Lernprojekt Zweiganggetriebe (3): Lösungen 09.12.2015, 05:43
Lösungsvorschläge zu den Aufgaben des Lernprojekts Zweiganggetriebe: Wie verläuft der Kraftfluss in den beiden Gängen? Achsabstände, Zähnezahlen, Übersetzungsverhältnisse und Übermaße berechnen, eine Zeichnung in Ansichten herstellen.
Lernprojekt Zweiganggetriebe: Aufgaben-Lösungen
Aufgaben
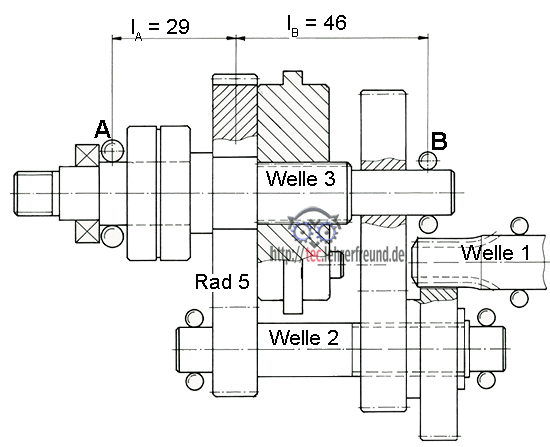
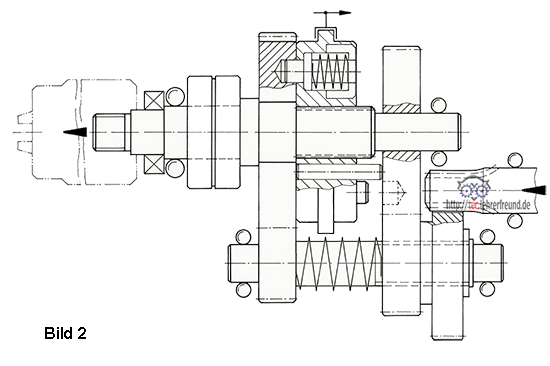
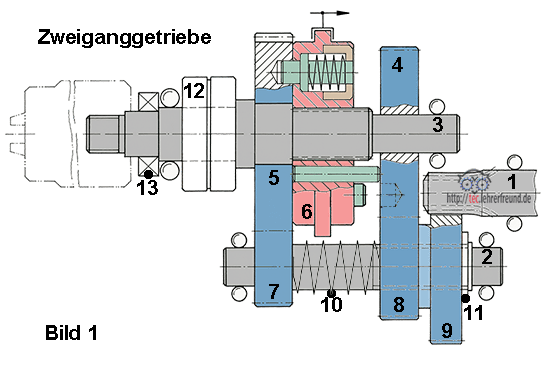
1. Drucken Sie die Getriebezeichnung aus und tragen Sie ein:
1.1 den Kraftfluss im langsamen Gang
1.2 den Kraftfluss im schnellen Gang
2. Beschreiben Sie die Abläufe der Kraftflüsse in beiden Gängen. Welche Funktion haben die Teile 6.1, 6.2 und 6.3 (Bild unten)? Wozu braucht man die Feder 10 und die Scheibe 11?
Kraftfluss: Der gedankliche Verlauf von Kräften in Baugruppen ist der Kraftfluss. Krafteinleitungsstellen sind die Punkte, an denen Kräfte von außen ein Bauteil belasten. Lager übertragen die Kräfte auf Nachbarbauteile.
3. Die Motorwelle dreht mit 1500 Umdrehungen pro Minute.
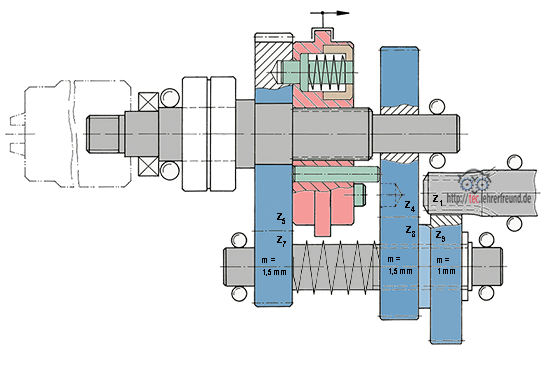
Die Räder 1 und 9 sind mit m = 1 mm verzahnt.
Die Räder 8 - 4 und 7- 5 sind mit m = 1,5 mm verzahnt.
z1 = 9
z9 = 30
z8 = 35
z7 = 26
z4 = 57
z5 = ? (berechnen, siehe 3.2)
3.1 Berechnen Sie die Achsabstände a1-9 und a8-4
3.2 Wie viele Zähne hat Rad 5?
3.3 Welche Übersetzungsverhältnisse werden in den beiden Gängen erreicht? Mit welchen Drehzahlen läuft die Bohrspindel im langsamen und schnellen Gang?
3.4 Welche Zahnkraft wirkt am Rad 4? Schneller Gang: Welches Drehmoment überträgt die Muffe auf die Abtriebswelle?
Lösungsvorschläge 1. bis 3.5
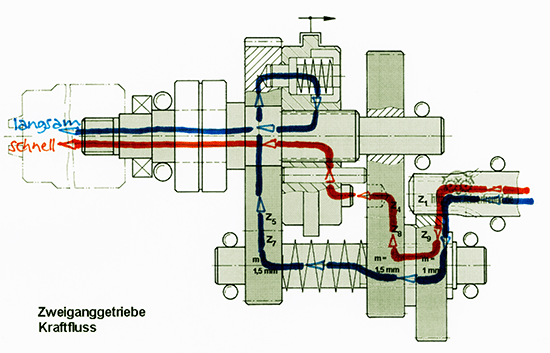
1. Kraftflüsse
Skizze: 1.1 Kraftfluss im langsamen Gang: Blaue Linie
1.2 Kraftfluss im schnellen Gang: Rote Linie. (Zunächst muss man den Verlauf abschätzen. Man sieht aber, dass die Räder 7 und 5 eine größere Übersetzung ergeben, dass Rad 5 also langsamer läuft als Rad 4.
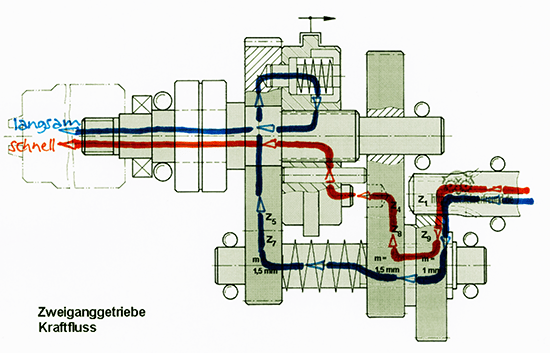
2. Beide Gänge laufen über die Schaltmuffe 6, d. h. die Zahnräder selbst werden beim Schalten nicht verschoben.
Schneller Gang: Die Schaltmuffe wurde nach rechts geschoben und wird deshalb von Zahnrad 4 mitgenommen. Die Schaltmuffe gibt ihre Bewegung über die Kerbverzahnung an die Abtriebswelle weiter. Das Stirnrad 5 läuft leer mit.
Beim Schalten der Muffe liegt der Mitnehmerbolzen 6.2 zunächst am Rad 4 an. Wenn die gestrichelt gezeichnete Bohrung im Zahnrad 4 erscheint, rastet der von der Feder gedrückte Mitnehmerbolzen ein und wird vom Rad 4 mitgenommen.
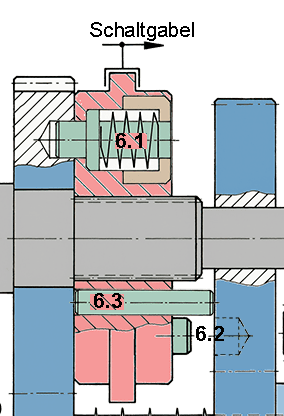
Langsamer Gang: Die Schaltmuffe wurde nach links geschoben; Mitnehmerbolzen 6.1 wird von Zahnrad 5 mitgenommen. Die Schaltmuffe gibt ihre Bewegung über die Kerbverzahnung an die Abtriebswelle weiter. Das Stirnrad 4 läuft leer mit.
Die Feder 10 sorgt dafür, dass der Zahnradblock 8 - 9 nach rechts geschoben wird. Die Scheibe 11 mit dem anschließenden Sicherungsring DIN 471 stützt den Zahnradblock ab.
3.1 Achsabstand 1-9:
a1-9 = (z1 + z9) : 2 • m = (9 + 30) : 2 • 1 mm =
a1-9 = 19,5 mm
a8-4 = (z8 + z4) : 2 • m = (35 + 57) : 2 • 1,5 mm =
a8-4 = 69 mm
3.2 Zähnezahl z5
Der Achsabstand a7-5 ist derselbe wie a8-4 = 69 mm. Wir berechnen deshalb z5 über die Achsabstandsformel a7-5 = a8-4 = (z7 + z5) : 2 • m. Diese Formel stellen wir nach z5 um:
z7 + z5 = a7-5 • 2 : m ––> z5 = a7-5 • 2 : m – z7 = 69 mm • 2 : 1,5 mm – 26 =
z5 = 66 Zähne
3.3 Abtriebs-Drehzahl n2 im schnellen Gang Rad 1 – 9 – 8 – 4. n1 = 1500 1/min
z1 = 9
z9 = 30
z8 = 35
z7 = 26
z4 = 57
z5 = 66
n2 = n1 : iges ––> iges = z9 : z1 • z4 : z8 = 30 : 9 • 57 : 35 = 5,43
n2 = 1 500 1/min : 5,43 = 276,32 1/min
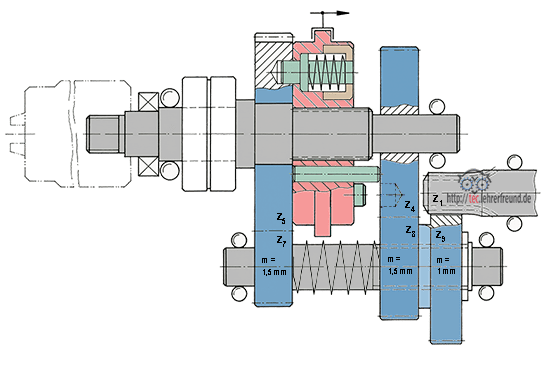
Abtriebs-Drehzahl im langsamen Gang Rad 1 – 9 – 7 – 5:
n2 = n1 : iges ––> iges = z9 : z1 • z5 : z7 = 30 : 9 • 66 : 26 = 8,462
n2 = 1 500 1/min : 8,462 = 177,27 1/min
3.4
– Zahnkraft am Rad 5
– Schneller Gang: Welches Drehmoment überträgt die Muffe auf die Abtriebswelle?
3.5 Die Motorwelle mit dem Ritzel z1 dreht mit 1 500 1/min. Die Antriebsleistung ist 1 200 Watt.
Zu berechnen für den langsamen Gang sind
– die an den Wellen I, II III entstehenden Drehmomente (siehe u. A. Zähnezahlen 3.)
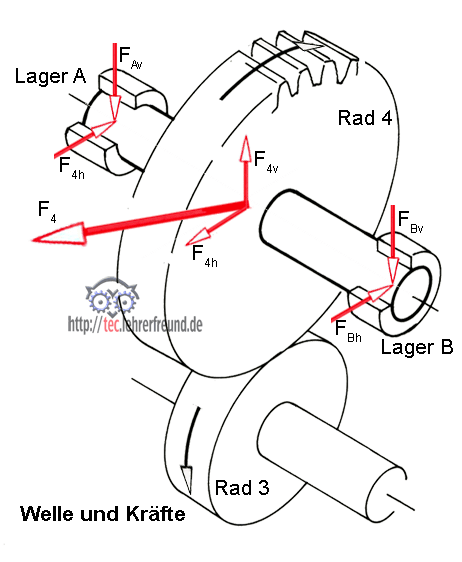
– die in A und B wirkenden Lagerkräfte. Vernachlässigen Sie dabei den Zahn-Eingriffswinkel.
Hilfe finden Sie unter »Getriebewelle berechnen«
Drehmomente:
MI = P1 • 9550 : n1 = 1,2 • 9550 : 1500 = 7,64 Nm
MII = MI • i1-9 = 7,64 • 30/9 = 25,47 Nm
MIII = MII • i7-5 = 25,47 • 66/26 = 64,65 Nm
Die Schaltmuffe 6 überträgt MIII
Die in A und B wirkenden Lagerkräfte ergeben sich anteilig aus F5:
F5 = MII : d5/2 ––> d5 = z5 • m = 66 • 1,5 mm = 99 mm
F5 = 64,65 Nm • 2 / 0,099 m =
F5 = 1 306 N
M linksdrehend = M rechtsdrehend
FA • 75 mm = F5 • 46 mm
FA = 1 306 N • 46 mm /75 mm
FA = 801 N
FB = 1306 N – 801 N =
FB = 505 N
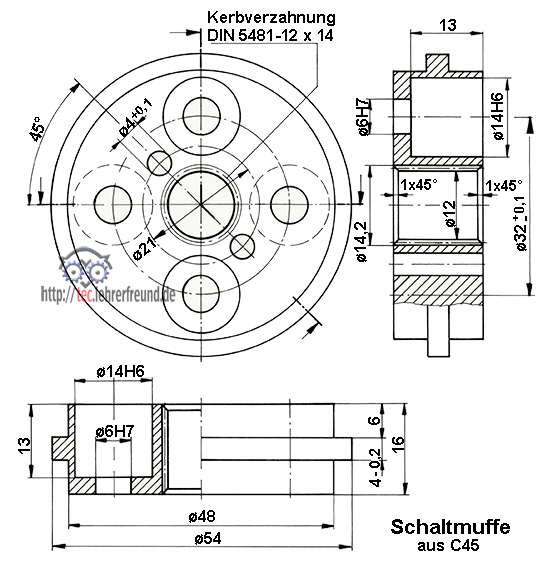
4. Stellen Sie von der Schaltmuffe 6 eine Zeichnung her. Keine Oberflächenangaben.
Weitere Angaben zur Schaltmuffe:
Der auf der Muffe sitzende mittige Schaltring ø 54 ist 4 –0,2 mm breit.
Die Bohrungen auf dem Lochkreis ø21 haben einen Durchmesser von 4 mm.
Der Lochkreisdurchmesser für die Mitnehmer ist höchstens 32,1 mm groß und mindestens 31,9 mm.
In die Bohrungen ø14 werden Buchsen gepresst; ihr Durchmesser 14p6. Berechnen Sie die beim Einpressen vorhandenen Übermaße, wenn die Bohrung in der Schaltmuffe mit H6 gefertigt wird.
Lösungsvorschlag
Passungsberechnung Schaltmuffe – Buchsen (4 Stück):
Bohrung 14H6
Oberes Abmaß +11
Unteres Abmaß 0
Buchsen-Außendurchmesser 14p6
Oberes Abmaß +29
Unteres Abmaß +18
Minimales Übermaß 0,007 mm
Maximales Übermaß 0,029 mm
____________________________
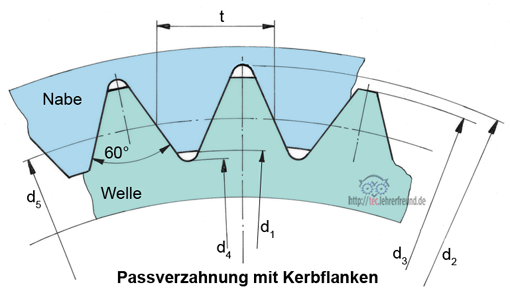
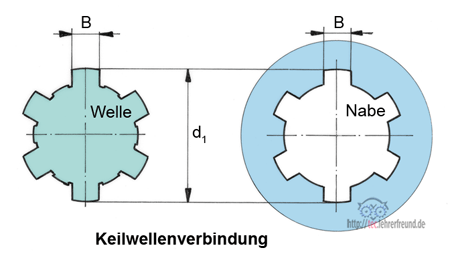
Das Kerbzahnprofil ist nach DIN 5481 genormt. Die Verbindung ist leicht lösbar und feinverstellbar. Verwendung zum Beispiel in Zahnradgetrieben, bei Achsschenkeln und Drehstabfedern an Kraftfahrzeugen. Die als „Keilwellenprofil“ genormte Mitnehmerverbindung ist ein Vielnutprofil. Die Bezeichnung „Keilwellenprofil“ ist irreführend, weil es in seiner Wirkungsweise der Passfederverbindung entspricht, nicht aber der Keilverbindung.
Die Verbindung ist leicht lösbar und achsial verschiebbar. Verwendung zum Beispiel bei Verschieberädergetrieben, bei Kraftfahrzeugkupplungen und Antriebswellen von Fahrzeugen.