Räumlicher Weihnachtsstern: Wie ist er aufgebaut? 13.01.2011, 07:19

Über Straßen gespannt und an Privathäusern leuchten in der Weihnachtszeit oft kunstvoll geformte, vielstrahlige Sterne. Immer wieder fragt man sich, wie es in ihrem Inneren aussieht, wo die Strahlen präzise und ohne Zwischenraum zusammenstoßen. Der tec.LEHRERFREUND lüftet das Geheimnis in kleinen Schritten.
Räumlicher Weihnachtsstern: Wie ist er aufgebaut?
Gespräch beim Einpacken eines Weihnachtssterns.
Kaspar, Melchior und Balthasar räumen die Weihnachtssachen auf. Darunter ist ein prächtiger Stern mit vielen Strahlen.
Kaspar: Wie sie den Stern wohl gemacht haben?
Melchior: Sie haben Sternstachel gebastelt und sie am dicken Ende zusammengeleimt.
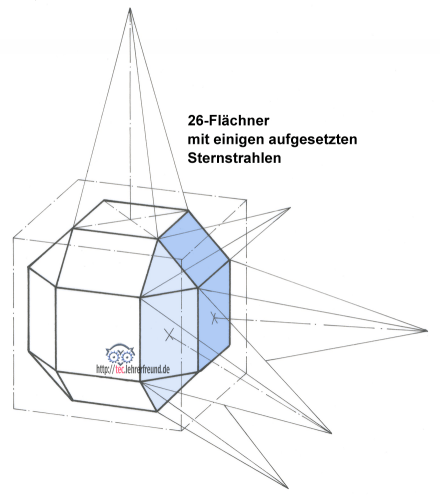
Balthasar: Du meinst die Sternstrahlen! Zusammengeleimt? Ganz so einfach wird es dann doch nicht gewesen sein. Ich habe gerade gezählt: Unser Stern hat immerhin 26 Strahlen.
C: Die Strahlen sind Pyramiden mit quadratischer Grundfläche.
M: Nicht alle! Ein paar davon, acht, haben eine dreieckige Grundfläche.
B: Dieser Stern artet mir zu einem mathematischen Problem aus.
C: Sagen wir, zu einem geometrischen.
M. Warum?
C: Weil die Strahlen in der Mitte des Sterns auf einen Würfel stoßen, genauer gesagt, auf einen speziellen Würfel. Würden die Strahlen auf einen normalen Würfel stoßen, dann hätten nur 6 davon Platz.
B: Das ist mir zu hoch. Könnt Ihr mir nicht so einen Würfel skizzieren? Caspar, du bist unser Zeichner: Hier hast du ein Blatt Papier und einen Bleistift.
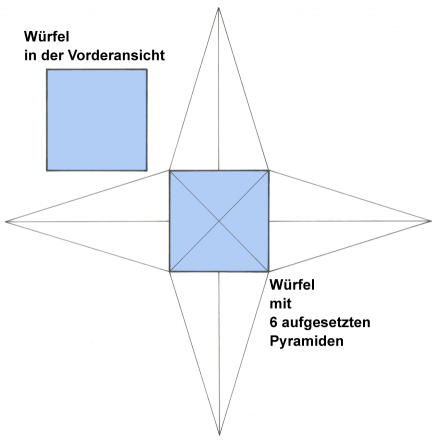
C (zeichnet): Dies wäre ein Würfel. Ihr könnt auch Sechsflächner oder Hexaeder dazu sagen.
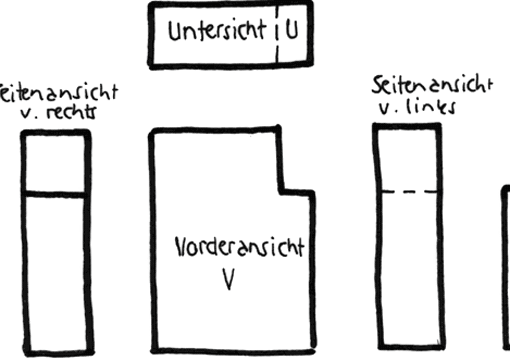
M: In der Vorderansicht ...
C: Richtig! Es könnte aber auch die Seitenansicht oder die Draufsicht sein. Beim Würfel haben alle drei Ansichten dieselbe Form. Auf jeder der 6 Flächen sitzt ein Sternstrahl; der unten liegende Strahl ist verdeckt.
B: Zeichne das doch mal perspektivisch!
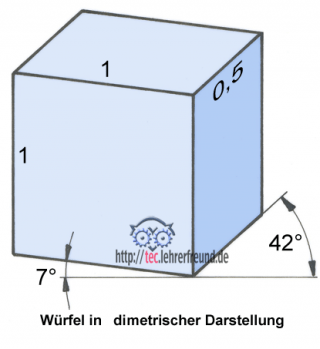
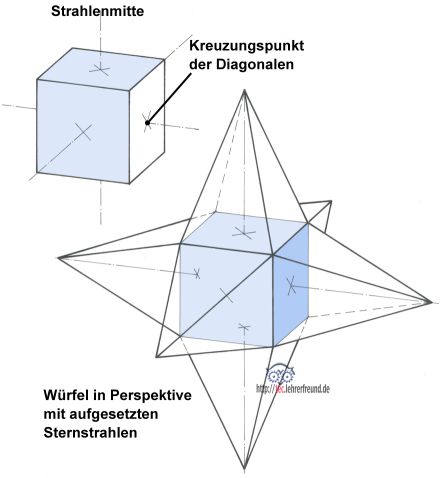
C: Wenn du meinst. Oben ist der Würfel, in dimetrischer Darstellung, falls du´s genau wissen willst. Seine Seiten stehen nach Norm im Verhältnis 1 : 1: 0,5. Für die Strahlenlängsachsen benötigen wir die Flächenmitten. Sie liegen im Kreuzungspunkt ihrer Diagonalen.
Und jetzt, Balthasar, wie machen wir weiter?
B: Wir müssen ja 26 Sternstrahlen unterbringen. Dafür brauchen wir auf dem Würfel 26 Flächen.
M: Wie wär´s, wenn wir die Kanten des 6-Flächen-Würfels abschrägen würden?
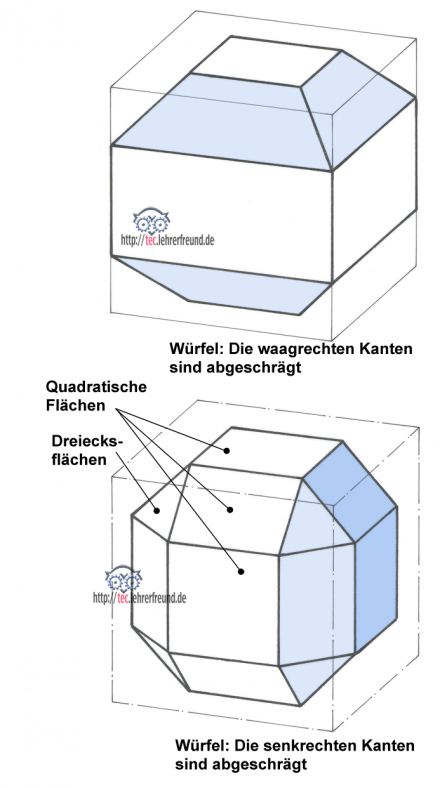
C: Meinst du, so?
Ich habe die waagrechten Kanten so abgeschrägt, dass oben und unten quadratische Flächen übrig bleiben. Alle anderen Flächen besitzen eine Rechteck- oder Trapezform.
M: 12 Rechtecke sind es; wir brauchen aber 26. Wenn nicht alle Flächen quadratisch sind, müssen auch die senkrechten Kanten abgeschrägt werden.
C: Damit nähert sich unser »spezieller« Würfel einer Kugel an. Das Ebenfeilen der 8 Dreiecksflächen ist der letzte Arbeitsgang.