Sammlung von Verständnis- und Einprägehilfen (2) 26.05.2008, 12:16

Hier gibt es Versuche zu Kreuzhiebfeilen, Schneidengeometrie, Evolvente, Modul.
 Der Trick mit den vesetzten Zähnen
Der Trick mit den vesetzten Zähnen
Kreuzhiebfeilen
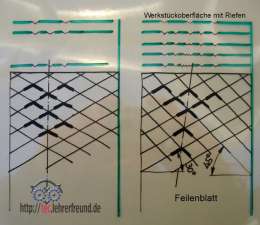
Für harte Metalle wie Stahl, Grauguss oder Stahlguss verwendet man Feilen mit Kreuzhieb. Dieser entsteht durch Einhauen eines tiefen »Unterhiebs« (hier 30°) und des darüberliegenden »Oberhiebs« (hier 45°) in das glühende Feilenblatt. Da die beiden Hiebe unterschiedlich zur Feilenachse geneigt sind, kommen hintereinander stehende Feilenzähne schräg zur Feilenachse zu liegen (Folie rechts). Dieser Trick verhindert beim Feilen, dass die aufeinanderfolgenden Zähne immer wieder auf dieselbe Riefe treffen. Die hintereinander versetzten Zähne bewirken vielmehr ein gleichmäßiges Abtragen von Spänen über die Feilenblattbreite.
Im Freihandversuch werden die Zahnspitzen aus den hintereinander liegenden Zahnreihen auf die darunter liegende grüne Folie projiziert. So zeigen sie, wie die zwischen den drei ersten Riefen liegende, noch nicht befeilte Fläche nach und nach abgetragen wird.
Schneiden oder schaben, das ist die Frage
Schneidengeometrie
Warum schabt ein Werkzeug (nur) und warum schneidet das andere?
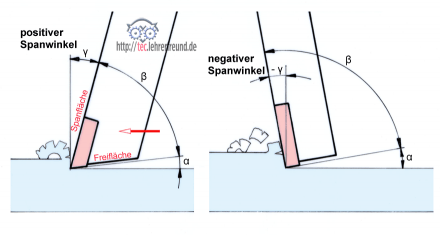
Das hängt mit der Schneidenform des Werkzeugs zusammen: Ist sein Spanwinkel γ positiv, dann kann die Schneide sich in das zu bearbeitende Material einkrallen und richtige Späne erzeugen. Ist er negativ wie in der Skizze rechts, hängt er also gewissermaßen in die Werkstückfläche hinein, dann entsteht beim Spanen lediglich ein besseres Pulver, eben Schabspäne.
Wachs zusammen mit einem Kerze und Küchenmesser sind für den schnellen Schulversuch ein geeignetes Gespann, dies schnell und eindeutig zu klären. Dabei ergibt sich der Spanwinkel durch die Messerneigung.
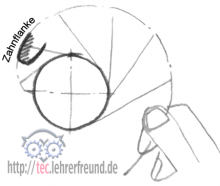
Kein Zahn ohne Evolvente
Die Evolvente, eine nicht leicht zu durchschauende Kurve, kommt zustande, wenn man um einen Zylinder (es könnte etwa der im Klassenzimmer stehende Papierkorb sein) einen Bindfaden - warum nicht auch das in der Nähe hängende Handtuch? - wickelt und es, den Zylinder an die Tafel gedrückt, unter Zug abrollt.
Führt man beim Abrollen eine Kreide mit, dann hat man die originale Evolvente an die Tafel gezeichnet.
Drehmomente verändern
Großer Radius, hohes Drehmoment
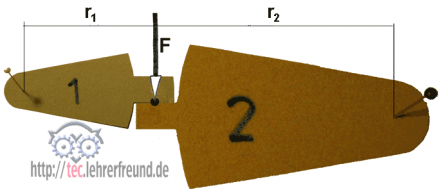
Auch das Verhalten des Drehmoments in Zahngetrieben lässt sich Erfolg versprechend im Gedankenversuch klären: Drückt Zahn 1 mit der Kraft F, dann überträgt er genau diese Kraft auf Zahn 2. Das am Rad 1 erzeugte Drehmoment F · r1 wird am Rad 2 vergrößert auf F · r2.
Der Modul (DIN 780)
Dem π ein Schnippchen schlagen (π = pi)
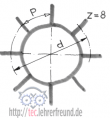 Die Grundformel der Zahnradberechnung entwickeln wir natürlich zusammen mit den Schülern. Wir bedienen uns einer einfachen Skizze eines Zahnrads mit 8 Zähnen. Dass wir mit dem mittleren Durchmesser d rechnen, auf dem die Zahnteilung p liegt, legen wir zunächst einfach fest. Entsprechend der Teilung heißt der mittlere Durchmesser Teilkreisdurchmesser (d).
Die Grundformel der Zahnradberechnung entwickeln wir natürlich zusammen mit den Schülern. Wir bedienen uns einer einfachen Skizze eines Zahnrads mit 8 Zähnen. Dass wir mit dem mittleren Durchmesser d rechnen, auf dem die Zahnteilung p liegt, legen wir zunächst einfach fest. Entsprechend der Teilung heißt der mittlere Durchmesser Teilkreisdurchmesser (d).
Wie kann man den den Umfang berechnen?
1. U = d • π
2. U = z • p
Aus d • π = z • p folgt: d = z • p/π
Der Bruch p/π erhält den Namen Modul m (lat. modus = Maßstab oder Maß); diese Größe wurde genormt und ist in einfachen Zahlenwerten abgestuft: 1, 2, 2,5 , 3, 3,5 ... usw. Also:
d = m • z
Damit ist das sehr unbequeme π aus der Zahnradberechnung ausgemerzt. Der Vorteil des genormten Moduls: Ist der Modul ganzzahlig, dann ergeben sich auch ganzzahlige Werte für den Teilkreisdurchmesser und für die Achsabstände.
Wenn nur noch 1 Zahn vorhanden ist
Keine Verklemmung
Die guten Eigenschaften der Evolvente lassen sich mit einfachen Versuchen kaum nachprüfen. Dagegen kann man beweisen, wie schlecht Zahnräder zusammenarbeiten würden, wenn deren Zähne parallele Flanken besäßen. Allerdings lässt das Modell nur erahnen, dass sich - neben den anderen Nachteilen - solche Zähne beim Laufen verklemmen müssten.
Im Freihandversuch a bis e werden einzähnige »Zahnräder« (aus Pappe, Sperrholz, Overheadfolie) in verschiedene Positionen gedreht.
Rad 1 ist das treibende, Rad 2 das getriebene Rad.
Das Übersetzungsverhältnis i = d2 : d1 = r2 : r1
Bilder
a: Das Übersetzungsverhältnis geht, weil r1 < r2, ins Langsame.
Das steigert sich in b) und c). In c) setzen die beiden Flanken schlagartig aufeinander auf, was in einem realen Getriebe bestimmt einen ziemlichen Lärm bedeuten würde. Ab c) - und klar erkennbar in d) - haben wir plötzlich eine Übersetzung ins Schnelle. Es ergibt sich also nur wegen der Flankenform innerhalb einer Umdrehung einmal ein schnellerer und einmal ein langsamerer Abtrieb. Der Fall wäre in der Praxis völlig undenkbar.
Zwischen d) und e) kann man auch die starke gleitende Reibung der Ecke r1 zeigen.

Wird fortgesetzt mit
Sammlung von Verständnis- und Einprägehilfen (3)
![]() Sammlung von Verständnis- und Einprägehilfen (1)
Sammlung von Verständnis- und Einprägehilfen (1)