Sammlung von Verständnishilfen (1) 04.06.2008, 19:32

Zu dieser Sammlung (mit Fortsetzungen) haben Generationen von technischen Lehrern Ideen beigesteuert. Den Unterricht interessant gestalten mit Versuchen zu Reiben, Antriebe mit Gasen und Flüssigkeiten, Drehmoment, Schiefe Ebene.
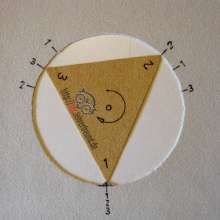
Reibahlen
Unregelmäßiges Gebiss
Mit Reibahlen will man sehr genaue Bohrungen herstellen. Das geht nur, weil sie selbst präzise und durchdachte Werkzeuge sind, die in der Vorbohrung vorhandene Ungenauigkeiten wie Rattermarken ausbügeln und auch selbst nichts derartiges fabrizieren. Dies ergibt sich insbesondere aus einer ungleichmäßigen Zahnteilung.
Hat eine Reibahle etwa 6 Zähne, dann wäre die regelmäßige Zahnteilung 6 x 60° (= 360°). Das Problem: Trifft ein Zahn auf eine Unebenheit wie eine Rattermarke oder eine harte Stelle in der Bohrungswandung, dann würde man wünschen, dass er diese Unebenheit weg reibt. Es könnte aber auch passieren, dass er die anderen 5 Zähne so in die Gegenrichtung drückt, dass auch sie Unebenheiten erzeugen. Jeder weitere auf die ursprüngliche Rattermarke auflaufende Zahn würde wieder dafür sorgen, dass die 5 gegenüber liegenden die bereits vorhandenen Vertiefungen vergrößern. Dem schiebt die ungleichmäßigen Zahnteilung einen Riegel vor.
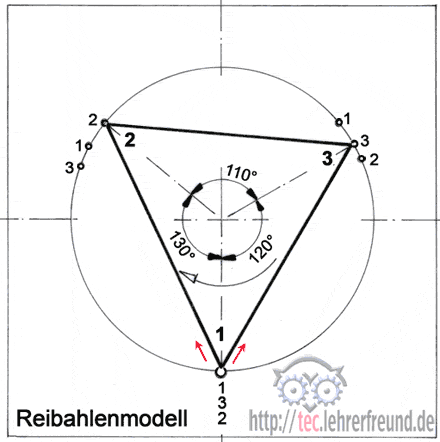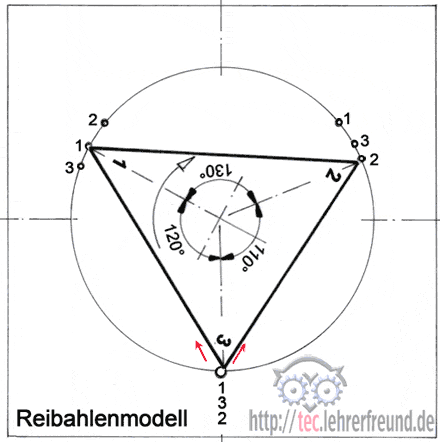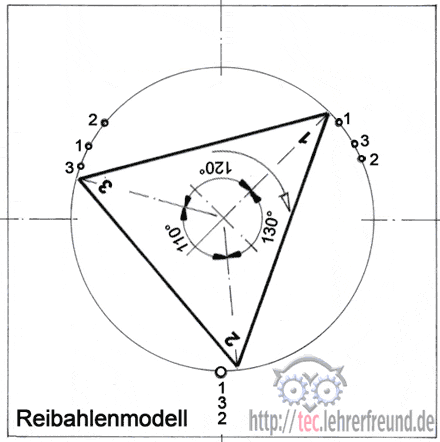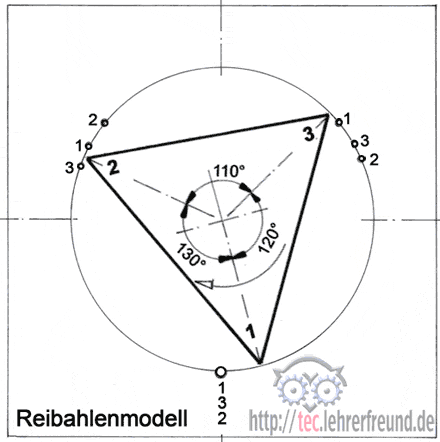
Sich dieses geometrische System mit seinen Auswirkungen vorzustellen, ist nicht einfach. Deshalb klären wir es mit dem denkbar einfachsten (aber nicht ganz optimalen) Reibahlenmodell. Es hat nur 3 Zähne, die im Abstand 110, 120 und 130° angeordnet sind. Beim Drehen in der Bohrung stellen wir einen Zahn auf die Erhebung unten und markieren eine Umdrehung lang die zwei anderen Zahnspitzen auf der Gegenseite: Sie sind drei Mal versetzt.
Der Versuch hat mehr Bedeutung als man denkt. Er fördert schon im 1. Jahr das Verständnis für später zu behandelnde ähnliche Probleme: Ungerade Zähnezahlen bei Zahnrädern führen zu einem ruhigeren Lauf; ungerade Kolbenzahlen bei Hydropumpen verbessern den Gleichförmigkeitsgrad der Ölförderung.
Das Drehen am Modell sieht dann ungefähr so aus:
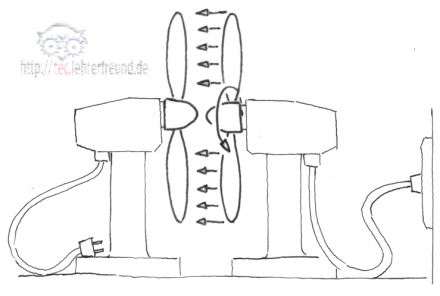
Sanfter Antrieb
Alles nur (heiße) Luft?
Stellt man zwei Ventilatoren gegeneinander und lässt einen laufen, dann treibt der entstehende Luftstrom langsam und ohne Ruck auch die Flügel des zweiten Ventilators an. Dies ist das Arbeitsprinzip der Strömungskupplung.
Wenn es im Unterricht passt, eignet sich der Versuch auch dafür, das Thema Kräfte, Kräfteparallelogramm und Kräftedreieck zu wiederholen.
Moment mal!
Drehmoment?
Die deutsche Sprache hat´s mit den Momenten: Ein Moment (männlich) ist ein kurzer Augenblick, das Moment (sächlich) ist ein Gesichtspunkt, ein Umstand.
Das Moment, das uns hier interessiert, meistens ein Drehmoment, ist keines von beiden. Es ist vielmehr eine Kraft, die zusammen mit einem Hebelarm einen Körper zu drehen versucht.
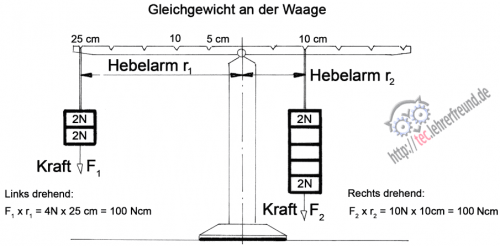
Was hier (und im Unterricht) zunächst abstrakt klingt, muss man natürlich mit einem Versuch verdeutlichen. Dazu sollte man schon einen Flachstab (kleines Bild) mit einer Bohrung in der Mitte und Abstandsmarkierungen, sowie Gewichte - am besten je 1 N - haben.
Ziel des Versuchs: den Hebel im Gleichgewicht halten. Dazu muss, egal wie viele Gewicht angehängt werden, jedes Mal die Summe der links drehenden Momente gleich sein der Summe der rechts drehenden Momente. Hier also:
Ml = Mr
F1 · r1 = F2 · r2
Die Vertiefung des Themas geschieht durch Anhängen weiterer Gewichte, zu denen die Schüler jeweils eine Möglichkeit des Drehmomenten-Ausgleichs angeben. Diese Übung stärkt das Kopfrechnen.
Eine Kräfteaufteilerin:
Die Schiefe Ebene
Schiefe Ebenen kommen in der Technik überall vor: Fahrzeuge fahren Steigungen hinauf oder hinab, Schraubenmuttern gleiten auf Gewindegängen, wenn sie angezogen oder gelöst werden, Maschinenwangen stehen schräg, um Schnittkräfte optimal aufzufangen.
Der hier beschriebene Gedankenversuch dazu kann eigentlich kaum einen Schüler überfordern. Ist er zu Ende gebracht, kann man die Überlegungen leicht mit einem Kraftmesser nachprüfen.
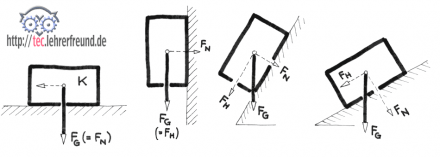
Der Versuch wird mit vier Tafelskizzen unterstützt:
1. Ein Körper K liegt auf einer ebenen Unterlage. Welche Kräfte wirken an K?
Das Gewicht FG. Weil es senkrecht auf die Unterlage drückt, heißt die Kraft auch FN (N = normal).
Kraft in horizontaler Richtung?
Keine Kraft (FH).
2. Die Unterlage wird senkrecht aufgestellt. Welche Kräfte wirken?
FG. Auf die Unterlage (senkrechte Wand) wirkt keine Kraft: FN = 0.
3. Die Senkrechte wird geneigt, z. B. um 60°. Kräfte?
FG (ist immer da). Jetzt wirken auch 2 Kräfte FN und FH, die aber jeweils kleiner sind als FG. FH > FN.
4. Die Schiefe Ebene wird weiter geneigt, so dass sie schließlich 30° mit der Waagrechten bildet. Kräfte?
FH ist kleiner als in Versuch 3; FN > FH. Beispiel Fahrrad.
Wird fortgesetzt mit
Sammlung von Verständnis- und Einprägehilfen (2)