Darstellende Geometrie: Punkte und Strecken projizieren 05.02.2014, 07:52
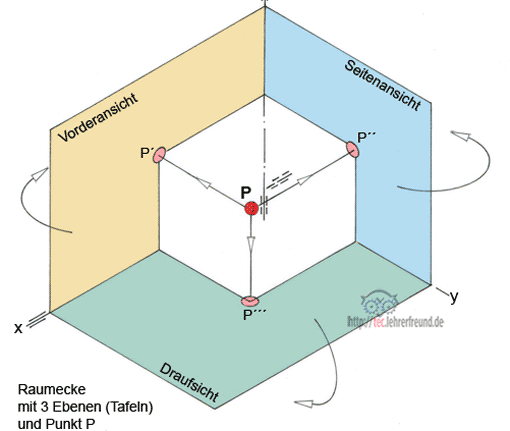
Die so genannte Dreitafelprojektion ist Grundlage für das zweidimensionale Abbilden von Körpern. Die ihr zugrunde liegende »Raumecke« kann als Ausschnitt aus einem Zimmer gesehen werden mit einem Fußboden und zwei aneinander stoßenden Seitenwänden. Diese Vorstellungshilfe ergibt die drei Ebenen, auf denen die Vorderansicht, die Seitenansicht und die Draufsicht des zu zeichnenden Objekts abgebildet werden.
Zeichnen mit der Dreitafelprojektion
Die darstellende Geometrie legt die Grundlagen für das Projektionszeichnen. Wenn ein räumlicher Gegenstand auf einer Fläche (z. B. einem Papierblatt) dargestellt werden soll, bedient man sich häufig der Dreitafelprojektion. Wie sie funktioniert, wird im Folgenden beschrieben.
Der Dreitafelprojektion liegt die »Raumecke« zugrunde. Sie kann als Teil eines Zimmers gesehen werden und würde dann aus dem Fußboden und zwei aneinander stoßenden Seitenwänden bestehen. Die Raumecke ist eine Vorstellungshilfe; ihre Wände ergeben, in die Zeichenebene auseinandergeklappt, die drei Ebenen, auf denen man die Vorderansicht VA, die Seitenansicht SA und die Draufsicht DS des zu zeichnenden Objekts abbildet.
Das Objekt wird senkrecht auf die Tafeln projiziert, daher der Begriff »senkrechte Parallelprojektion«. Mit dieser Methode erhält man maßgerechte Ansichten. Die zu den Ebenen gehörigen Achsen werden mit x, y und z bezeichnet.
1. Bild unten: Einen Punkt P projizieren
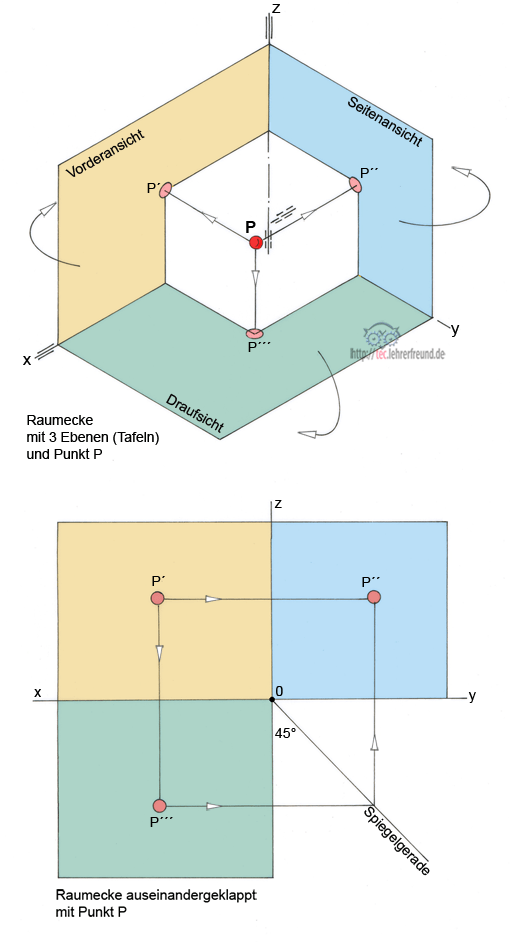
Wir bezeichnen die Projektion des Punkts P
- in der VA mit P´
- in der SA mit P´´
- in der DS mit P´´´
P´´ wird mit Hilfe der Spiegelgeraden bestimmt.
2. Bild unten: Eine Strecke AB projizieren
a) Die Stecke AB liegt parallel zu VA und DS.
Zum besseren Verständnis stellen wir AB als Zylinder dar. In den drei Projektionen zeichnen wir aber lediglich die Mittellinie des Zylinders.
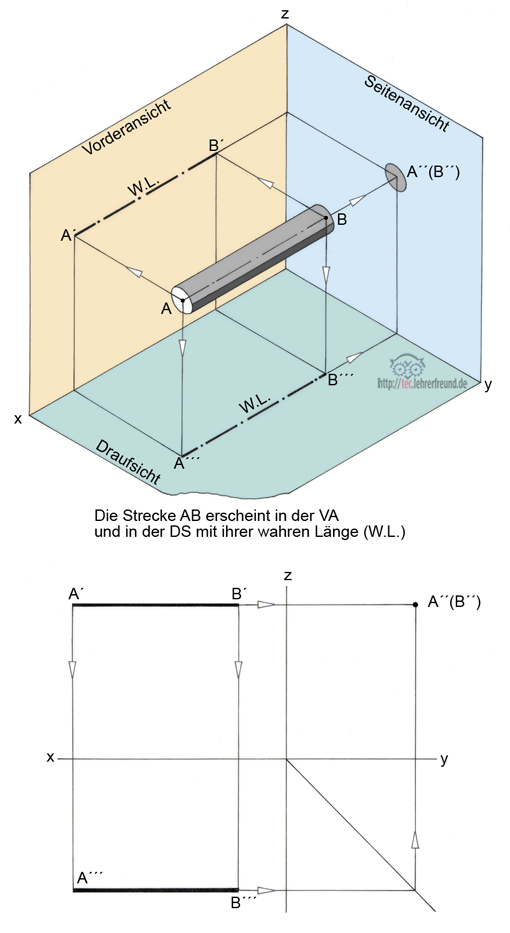
Die oben dargestellte Strecke AB liegt parallel zur VA und zur DS. In diesen beiden Ansichten bildet sich AB mit ihrer tatsächlichen oder »wahren« Länge ab. In der SA erscheint sie als Punkt.
b) Bild unten: Die Strecke AB liegt parallel zur Draufsicht, aber schräg zur Vorderansicht. Mit ihrer wahren Länge W.L. erscheint eine Strecke immer nur in der Ansicht, zu der sie parallel liegt. Hier ist es die DS. In VA und SA erscheint AB verkürzt.
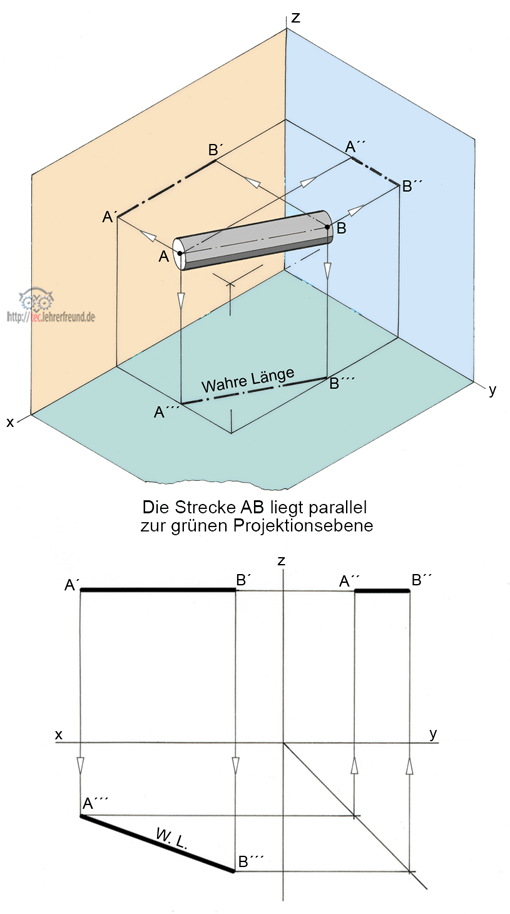
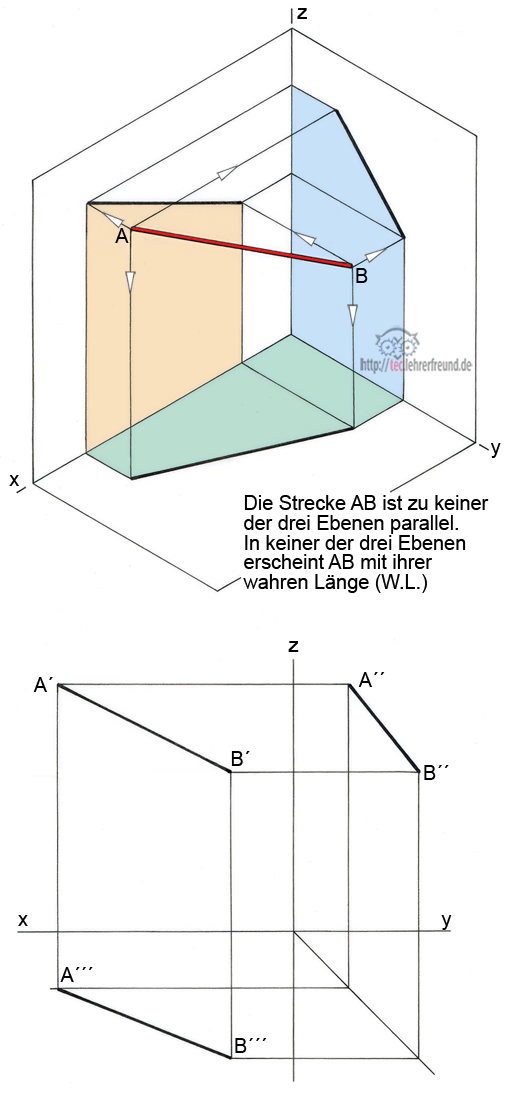
Bild unten: AB liegt zu allen drei Projektionsebenen schräg
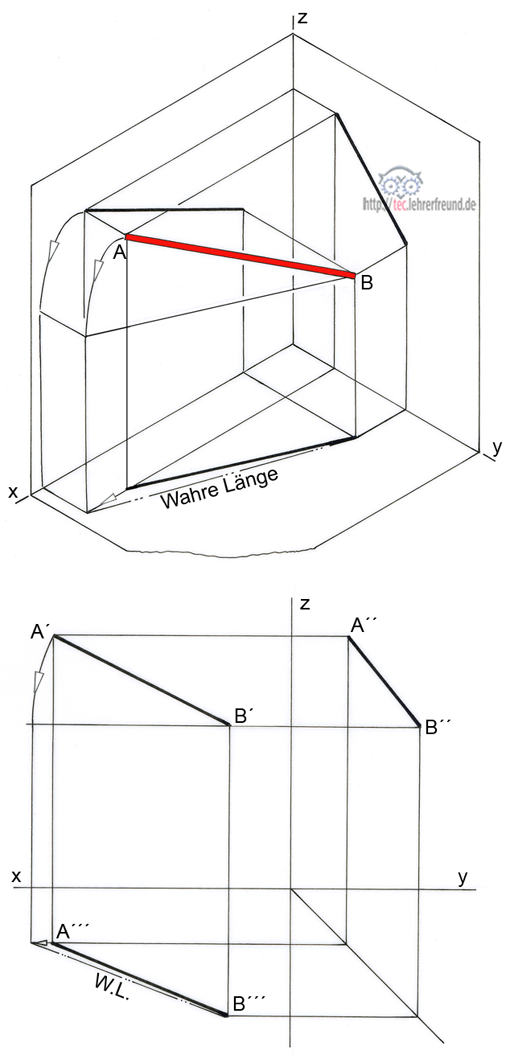
c) Bild unten: Die wahre Länge der Strecke AB finden
AB liegt zu allen drei Projektionsebenen schräg. In diesem Fall erscheinen alle drei Streckenprojektionen verkürzt. Eine Methode, die wahre Länge (W.L.) zu ermitteln, ist das Drehen einer der Strecken um einen Punkt. Im hier gezeichneten Beispiel wurde B als Drehpunkt gewählt. Dabei dreht man die verkürzte Strecke zum Beispiel in der VA durch Zirkelschlag so, dass sie parallel zur DS liegt. Dann ergibt sich die W.L. von AB als Verbindung zwischen B´´´ und dem durch Konstruktion gefundenen weiter außen liegenden Punkt.
3. Bild unten: Eine Fläche projizieren