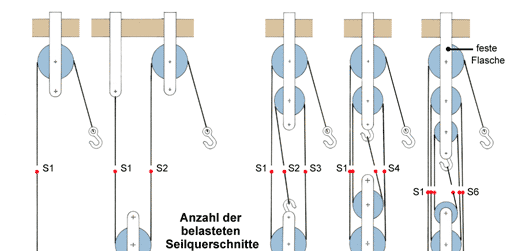
Flaschenzug (2) 25.01.2014, 07:18

Kraftübersetzungen bei Flaschenzügen erreicht man, indem man unterschiedliche Rollenzahlen und -anordnungen kombiniert. Einige der Arten zeigen die Aufgaben in diesem Beitrag.

Flaschenzüge 

Flaschenzüge und ähnliche Konstruktionen gibt es in den unterschiedlichsten Arten. Eine Auswahl zeigen die folgenden Aufgaben. 

Aufgaben 

Zugleuchte

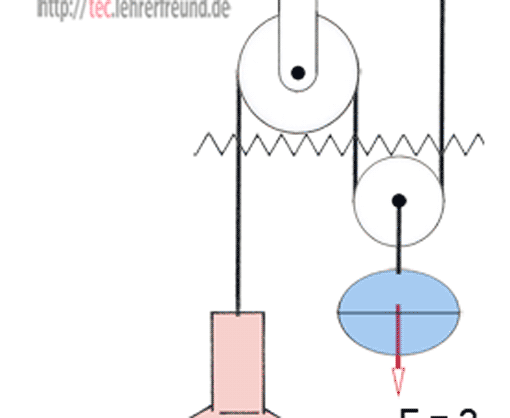
1. Zugleuchte: Die Leuchte ist höhenverstellbar und bleibt wegen dem Gegengewicht F in jeder gewählten Position stehen. 

a) Das Gewicht der losen Rolle soll ebenso unberücksichtigt bleiben wie die Reibung. Wie groß ist das Gewicht F des Gegengewichts? 
b) Die lose Rolle wiegt F = 3,0 N. Wie groß muss F jetzt sein? 

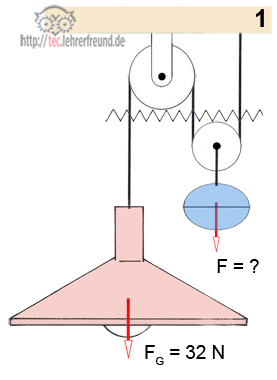
2. Flaschenzug. 

a) Berechnen Sie F_z.  
b) Am linken Seilende wird das Seil 2,1 m eingezogen. Wie hoch wird die Last F_G gehoben?  
c) Mit welcher Gesamtkraft wird die Decke belastet?

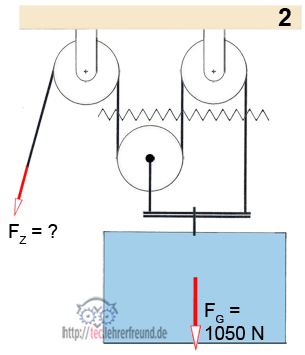
3.  Potenz-Flaschenzug.

a) Reibung, Rollen- und Seilgewicht bleiben unberücksichtigt. 
Welche Last F_G kann angehoben werden? 
b) Die beiden Rollen 1 und 2 wiegen jeweils 30 N. Wie groß ist F_G jetzt?  
c) Mit welcher Gesamtkraft wird die Decke belastet? 

Erläuterung: Der Potenzflaschenzug spart Kraft ausschließlich mit losen Rollen; das Seil jeder Rolle ist an der Stütze (Decke) und der nächsten Rolle befestigt. Mit der Anzahl der losen Rollen potenziert sich die Wirkung entsprechend folgender Formel: F_Z = F_G : 2ⁿ. n ist die Anzahl der losen Rollen.

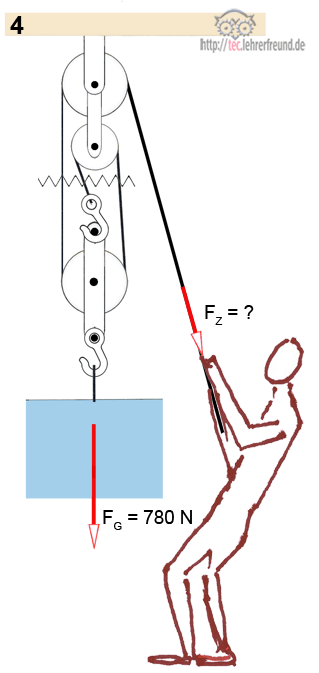
4. Flaschenzug

a) Reibung, Rollen- und Seilgewicht bleiben unberücksichtigt. Wie groß ist F_Z?  
b) Mit welcher Gesamtkraft wird die Decke belastet? 

_____________________

Lösungsvorschläge

1. Zugleuchte: Die Leuchte ist höhenverstellbar und soll in jeder gewählten Position stehen bleiben. 
a) Das Gewicht der losen Rolle soll ebenso unberücksichtigt bleiben wie die Reibung. Wie groß ist das Gewicht F des Gegengewichts? 
b) Die lose Rolle wiegt F = 3,0 N. Wie groß muss F jetzt sein?

a) Die Lampe zieht am linken Seilstrang mit 32 N. Dieselbe Belastung nehmen auch der mittlere und der rechte Seilstrang auf. F muss also 2 x 32 N = 64 N sein. 
b) F muss das Rollengewicht zusätzlich aufbringen. Dann bleibt für die Lampe weniger Zugkraft übrig: F = 64 N - 3 N = 61 N.  

2. Flaschenzug. Die Zickzacklinie soll eine Schnittebene darstellen. Es werden drei Seilquerschnitte belastet. 

a) Berechnen Sie F_z. 
b) Am linken Seilende wird das Seil 2,1 m eingezogen. Wie hoch wird die Last F_G gehoben?
c) Mit welcher Gesamtkraft wird die Decke belastet?

a) F_Z = F_G : 3 = 1050 N : 3 = 350 N

b) 3 mal mehr Kraft bedeutet, nur 1/3 Hubweg: Hubweg = 2,1 m : 3 = 0,7 m

c) Beim Ziehen hängt das Lastgewicht F_G = 1050 N an der Decke. Dazu kommen 350 N Zug am Seilende. Die Gesamtzugkraft an der Decke ist also 1400 N.

3. Potenz-Flaschenzug
a) Reibung, Rollen- und Seilgewicht bleiben unberücksichtigt. Welche Last F_G kann angehoben werden? 
b) Die beiden Rollen 1 und 2 wiegen jeweils 30 N. Wie groß ist F_G jetzt? 
c) Mit welcher Gesamtkraft wird die Decke belastet? 

a) Die Zugkraft F_Z = 320 N wirkt an beiden Seilsträngen der Rolle 1. Daraus ergibt sich, dass der rechte Seilstrang der Rolle 2 mit F = 640 N belastet wird. Das Gewicht F_G ist damit 2 x 640 N = 1280 N.

b) Weil die Rollen nach oben befördert werden müssen, kann weniger Last gehoben werden. Nach Rolle 1 ist die Kraft an dem über Rolle 2 laufenden Seil  640 N - 30 N = 610 N. Am Haken kommen nur noch 1220 - 30 N = 1190 N an.

c) Die Decke wird von der Gesamtlast 1190N + Rollengewicht 60 N + Seilzug 320 N = 1 570 N belastet. 
Kontrollrechnung: Das linke Seil belastet die Decke mit 610 N, das nächste Seil mit 320 N, über die feste Rolle werden 640 N in die Decke eingeleitet. Die drei Zahlen addiert ergeben 1570 N.

4. Flaschenzug 
a) Reibung, Rollen- und Seilgewicht bleiben unberücksichtigt. Wie groß ist F_Z?  
b) Mit welcher Gesamtkraft wird die Decke belastet? 

a) Die Schnittebene kreuzt 3 tragende Seilquerschnitte. Jeder übernimmt 780 N : 3 = 260 N. 
b) F_Z = 260 N. An der Decke zieht die Last 780 N + der Seilzug 260 N; das ergibt 1040 N.