Gleichgewichtslagen und Standsicherheit 20.02.2010, 18:48

Gleichgewichtslagen, Vorschaubild

Die Lage des Schwerpunktes eines Körpers in bezug auf seine Standfläche bestimmt seine Standsicherheit. Die Gleichgewichtslagen sagen etwas darüber aus, wie sicher oder «wackelig« ein Körper steht.

Anzeige
Anzeige
  • (geändert: )

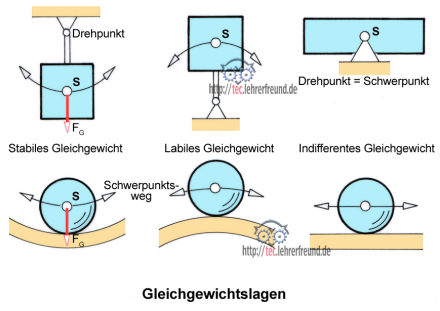
Gleichgewichtslagen

Die Lage des Schwerpunkts eines Körpers in bezug auf seine Standfläche bestimmt seine Standsicherheit. Man unterscheidet drei Gleichgewichtslagen, die mit einer auf unterschiedlichen Rollflächenformen liegenden Kugel verständlich illustriert werden können:
Liegt die Kugel in einer Schüssel (links unten), dann ist sie im stabilen Gleichgewicht: Nach einer Verschiebung wird sie zum tiefsten Punkt zurück rollen.
Liegt die Kugel auf einer Kuppe, dann ist sie im labilen Gleichgewicht: Durch Antippen wird sie weg rollen.
Liegt die Kugel auf einer Ebene, dann ist sie im indifferenten Gleichgewicht: S bleibt an dem Punkt liegen, an den man sie verschiebt. Eine einmalige Krafteinwirkung wird sie (bei Vernachlässigung des Reibungswiderstandes) in ihrem Bewegungszustand verharren lassen.

Gleichgewichtslagen

 

Obere Bildreihe
Stabiles Gleichgewicht: Der Körperschwerpunkt muss bei Lageänderung gehoben werden. Dazu ist eine bestimmte Hubarbeit nötig.
Labiles Gleichgewicht: Der Körperschwerpunkt senkt sich bei Lageänderung. Das Senkmoment wirkt unterstützend auf eine Veränderung der Körperlage.
Indifferentes Gleichgewicht: Bei Lageänderung bleibt der Schwerpunkt immer in gleicher Höhe.

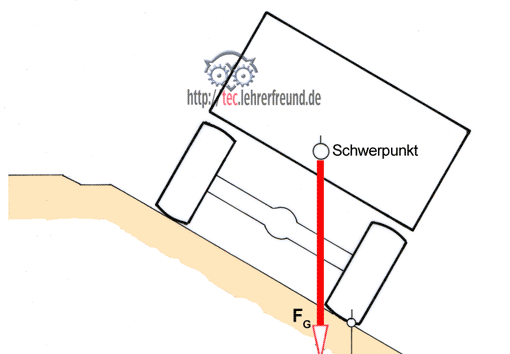
Standsicherheit

Die Standsicherheit ist die Anforderung an Maschinenteile, Maschinen oder sonstige Baukonstruktionen, nicht umzufallen oder einzustürzen. 

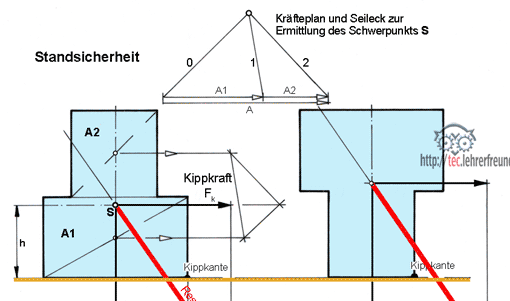
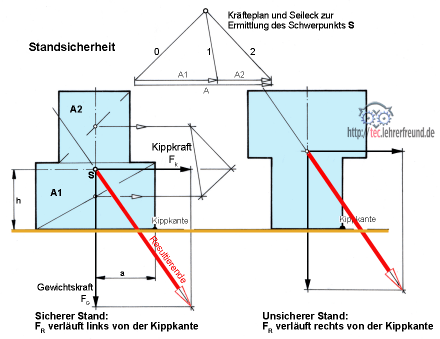
·Grundfläche und Standsicherheit

Bild: Derselbe Körper steht links auf der breiten Auflage, rechts auf der schmalen. Auf den Körper wirken das

Kippmoment Mk = Kippkraft Fk · Schwerpunkthöhe h
Mk = Fk · h  und das
Standmoment Ms = Gewicht FG · Standbreite a
Ms = FG · a

Verläuft die Resultierende aus Kippkraft Fk und Gewicht FG innerhalb der Standfläche, kann der Körper nicht kippen. Sicherheit gegen Kippen ist vorhanden, wenn das Standmoment Ms größer ist als das Kippmoment Mk. Der Grad der Sicherheit S wird durch das Momentverhältnis ausgedrückt:

Standsicherheit S = Ms : Mk = FG · a / Fk · h

_____________________

Übungsaufgaben dazu im nächsten Beitrag
 

Anzeige

Kommentare

8

Zum Artikel "Gleichgewichtslagen und Standsicherheit".

  • #1

    Hallo,
    gibt es für freistehende Regale im Nicht Wohnbereich, Angaben zum Kippmoment. Welche minimale oder maximale Vorgaben gibt es, um die Standsicherheit des Regals zu gewährleisten?
    Bitte um Rücksprache

    schrieb Fluhr am

  • #2

    Hallo,
    ich habe die Aufgabe die Standsicherheit eines Regals für Kleider zu überprüfen.
    Das Regal ist 1m breit, 0,5 m tief und 1,7 m hoch.
    das Standmoment ergibt sich mit (86N+400N)x0,85m=413 Nm
    Die Kraft ab wann das Regal kippt ist 413N/1,5m= 275N. das heißt ab einer Kraft von 275N die horrizontal in 1,5m angreift beginnt das Regal zu kippen. Mir fehlt die Beurteilung, ist dies ein guter Wert oder nicht ausreichend. Bitte um Rücksprache!

    schrieb Dieter am

  • #3

    Bienenstock hat 50x50 cm. Wenn ich ihn hinten hochhebe zeigt die Waage 20 kg. Der Kipppunkt ist die vordere Kante des Bienenstockes. Kann ich daraus schließen, dass das Gesamtgewicht 40 kg ist?

    schrieb Karl Fraißler am

  • #4

    Guten Morgen, Herr Schatz,

    vielen Dank für Ihre Mühe, die Sie sich um das Thema machen. Wir glauben, Sie schürfen damit tiefer als der tec.LEHRERFREUND. Aber lassen Sie auch uns darüber schlafen - vielleicht finden wir eine Ergänzung zu Ihren Ausführungen.

    Mit den besten Grüßen
    tec.LEHRERFREUND

    schrieb tec.LEHRERFREUND am

  • #5

    Guten Morgen, Herr tec.LEHRERFREUND,

    nachdem ich eine Nacht über das Problem geschlafen habe, ist es mir jetzt - glaube ich - klar geworden.
    1) Ihr Beispiel ist doch nicht so ganz perfekt, weil Sie in den beiden Darstellungen Äpfel mit Birnen vergleichen. Das Kippmoment im rechten Bild ist größer als im linken Bild.
    2) Unter quasistatischen Verhältnissen wird die Kippbewegung in dem Moment eingeleitet, da das Kippmoment größer wird als das Haltemoment, unabhängig von der Lage des Schwerpunktes.
    3) Unter quasistatischen Verhältnissen setzt der Körper der Kippbewegung so lange einen Widerstand entgegen bis der Schwerpunkt genau über dem Kipppunkt liegt.
    4) Dieser Widerstand besteht aus zwei Komponenten: Komponente 1 ist das Haltemoment mit reduziertem Hebelarm (weil der Schwerpunkt näher an den Drehpunkt rückt) und Komponente 2 ist die Zunahme an potentieller Energie, weil der Schwerpunkt bei der Drehbewegung nach oben verschoben wird (lässt sich auch als Moment ausdrücken: G * h, wobei h die Höhenverschiebung).
    5) Je nach Geometrie kann deshalb bei entsprechend niedriger Schwerpunkthöhe und großem Abstand zum Drehpunkt der Kippwiderstand sogar wieder anwachsen, was dazu führt, dass in der Bewegung das Kippmoment wieder kleiner als das effektive Haltemoment werden kann und die Bewegung zur Ruhe kommt (Prinzip Stehaufmännchen).

    Damit sollten aus meiner Sicht die Zusammenhänge jetzt geklärt sein.

    Vielen Dank für Ihre Anregungen.

    Mit freundlichen Grüßen

    Tino Schatz

    schrieb Schatz am

  • #6

    Hallo Herr tec.LEHRERFREUND,

    vielen Dank für die schnelle Antwort.
    Sie haben völlig recht - ich hatte übersehen, dass Sie die Kippkraft so angesetzt haben, dass sie im Schwerpunkt angreift.
    Üblicherweise (oder irre ich mich da?) wird doch aber die horizontale Kippkraft an der Stelle angesetzt, wo sie tatsächlich auftritt, zum Beispiel an der obersten Kante. Und dann wird doch meines Erachtens das Kippmoment so berechnet, dass man die angreifende Kraft mal dem Hebelarm bis zum Drehpunkt nimmt und dieses Kippmoment mit dem Standmoment vergleicht. Da das Standmoment unabhängig von der Schwerpunktlage bleibt und auch das so m.E. üblicherweise berechnete Kippmoment den Schwerpunkt nicht berücksichtigt, würde sich der Effekt des günstiger nach unten verschobenen Schwerpunktes nicht erfassen lassen. Also mir ist nicht bekannt, dass man sich das anzusetzende Kippmoment so ermittelt, als würde die H-Kraft im Schwerpunkt angreifen. Aber vielleicht können Sie mir dazu noch etwas erläutern?
    Viele Grüße
    Schatz

    schrieb Schatz am

  • #7

    Hallo Herr/Frau Schatz,

    Einspruch!

    Die Formel beachtet die Höhe h des Gesamtschwerpunkts schon.
    Annahme: h rutscht nach unten. Dies wäre beispielsweise der Fall, wenn bei gleich bleibender Körperform und gleichem Gesamtgewicht der untere Teilkörper aus Stahl und der obere aus Kunststoff bestünde. Das nun kleinere Mk und das gleich gebliebene Ms vergrößern die Standsicherheit S automatisch.

    Gruß
    tec.LEHRERFREUND

    schrieb tec.LEHRERFREUND am

  • #8

    Das Beispiel zur Standsicherheit ist ganz überzeugend, doch bleibt ein Aspekt unbeachtet, nämlich die Höhe des Gesamtschwerpunktes. Der bloße Vergleich von Kipp- und Standmoment ergibt beim linken Beispiel nämlich immer das Gleiche, egal, ob die Masse in A1 oder in A2 konzentriert ist. Tatsächlich reagiert ein Körper aber stabiler, wenn der Schwerpunkt weiter unten liegt. Dieser Effekt bleibt leider unberücksichtigt.

    schrieb Schatz am

Ihr Kommentar

zum Artikel "Gleichgewichtslagen und Standsicherheit".



Wir speichern Ihren Kommentar dauerhaft ab (was auch sonst?). Mehr dazu in unserer ausführlichen Datenschutzerklärung.

Andere tec.Lehrerfreund/innen lasen auch:

Anzeige
Nach oben

 >  646 Einträge, 952 Kommentare. Seite generiert in 0.3306 Sekunden bei 101 MySQL-Queries. 483 Lehrer/innen online (3 min Timeout / 1674 ) |