Durchdringungen: Zylinder durchdringt Kreisring außermittig 18.08.2010, 10:10
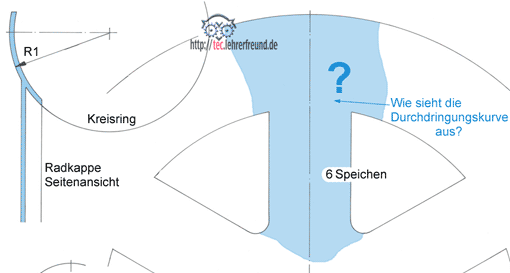
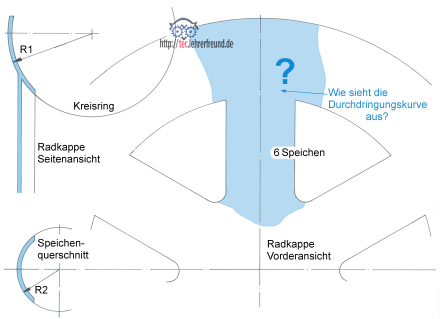
Ein Bauteil, das uns täglich begegnet und uns alle möglichen Durchdringungskurven bietet, ist die Radkappe an Personenwagen. Wir überlegen, wie man die Durchdringungskurve konstruiert, wenn der Außenring Teil eines Kreisrings ist, auf den radial sechs zylindrische Speichen stoßen.
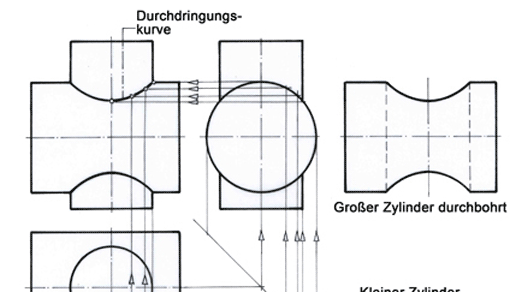
Durchdringung Zylinder mit Kreisring
Das Foto zeigt eine Radkappe, wie es sie in unzähligen Formen gibt. Radkappen - sie sind in der Regel aus Kunststoff - dienen der optischen Verschönerung der Räder; daneben schützen sie die Naben und Radmuttern vor Verschmutzung, und tragen zur Verringerung des Fahrwiderstandes bei. Radkappen werden meistens mit Schnappverbindungen an der Felge befestigt.
Viele Radkappen haben die Gemeinsamkeit, dass eine Anzahl von speichenartigen Formen mit dem äußeren Ring der Kappe verbunden ist.
Wir überlegen, wie man die Durchdringungskurve konstruiert, wenn die Außenpartie Teil eines Kreisrings ist, auf den sechs zylindrisch geformte Speichen treffen. Das Kugelschnitt-Verfahren kommt nicht in Frage, weil Zylinder und Kreisring sich nicht mittig durchstoßen. Hier muss man mit Schnittebenen arbeiten. Wie dieses Verfahren funktioniert, ist in einem früheren tec.LEHRERFREUND-Beitrag nachzulesen: Durchdringungslinien (2).
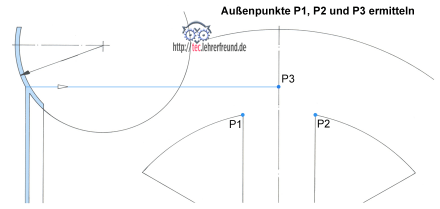
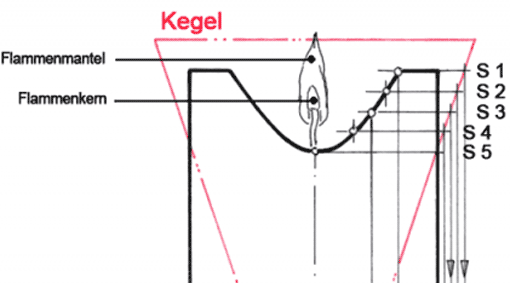
Im ersten Schritt ermitteln wir die Außenpunkte P1, P2 und P3 der Durchdringungskurve. Sie geben einen ersten Anhaltspunkt über deren Form. Weitere Punkte erhält man mit der Schnittmethode.
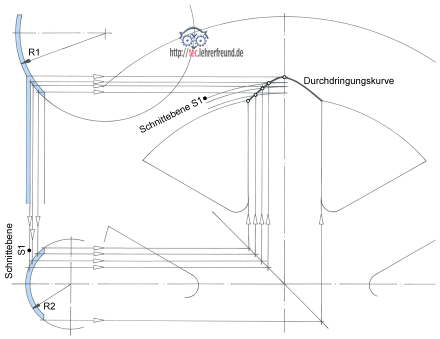
Im zweiten Schritt legen wir innerhalb der Außenpunkte Schnittebenen. Dazu benötigt man den Speichenquerschnitt als Draufsicht. Im kreisringförmigen Bereich der Radkappe bilden die Schnittebenen (z. B. S1) kreisrunde Scheiben. Die Projektion - verdeutlicht durch Pfeile - von der Seitenansicht in die Draufsicht und weiter in die Vorderansicht führt zu neuen Punkten. Durch sie verläuft die Durchdringungskurve.
Wichtig ist in der Vorderansicht, dass die Schnittebenen als Kreise dargestellt werden. Ohne diesen Schritt erhält man zwar eine ähnliche Kurve, aber nicht die genaue.
Eine weitere, vertiefende Übung wäre, die Zeichnung oben zu verwenden und darin den Speichenquerschnitt zu verändern, z. B. ihm ein trapezförmiges Aussehen zu geben. Dann ergibt sich natürlich eine veränderte Durchdringungskurve.