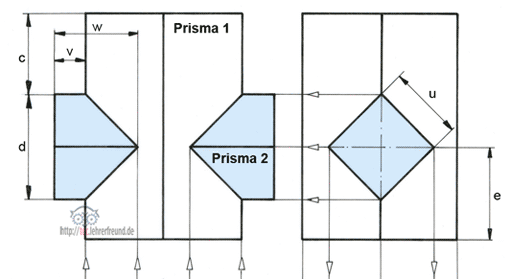
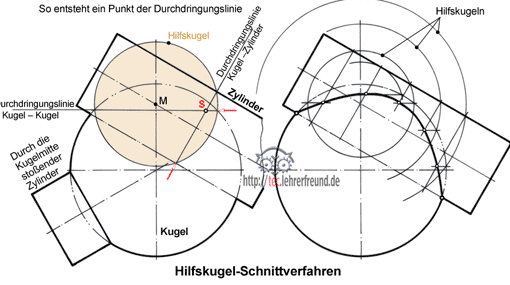
Durchdringungslinien (2) 17.06.2008, 17:13
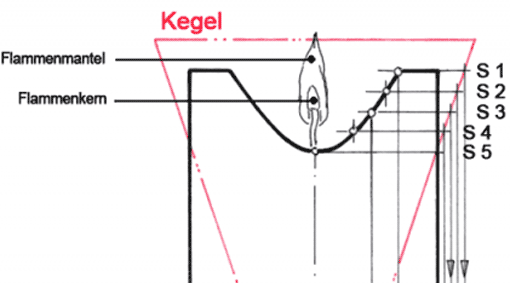
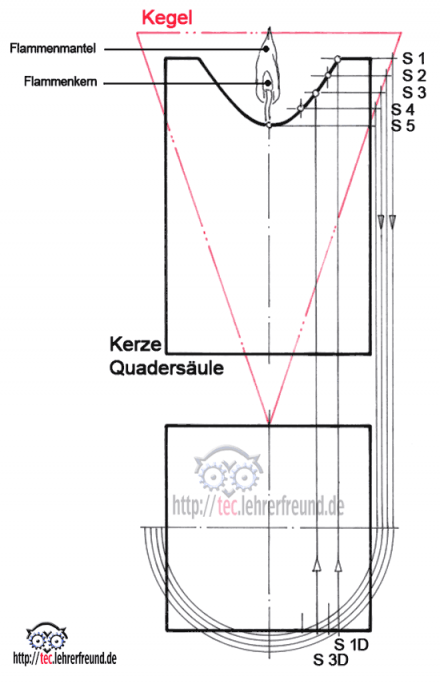
Brennende Kerze: Hier gehen wir von einer kegelförmigen Wärmeausbreitung aus. Dann ergibt sich als Schmelzlinie ( = Durchdringungslinie) eine Hyperbel.
Fortsetzung von Durchdringungslinien (1)
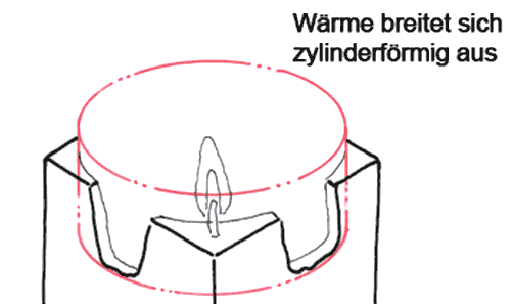
In Durchdringungslinien (1) hatten wir vermutet, die Hitze der der Kerzenflamme breite sich zylinderförmig aus. Wahrscheinlicher ist, dass die Wärme einen kegelförmigen Verlauf hat. Der Grund: Die Flamme ist nicht an jeder Stelle gleich heiß. In ihrem unteren Bereich und im Flammenkern ist die Verbrennung des Wachses unvollständig, was zur Folge hat, dass dort die Temperaturen niedriger sind als weiter oben.
Gehen wir also von einer kegelförmigen Wärmeausbreitung aus. Wie schmilzt dann die Kerzenwandung durch?
Vorgehensweise:
- Kerze in DS (Draufsicht) und VA (Vorderansicht) zeichnen.
- In die VA den vermuteten Kegel einzeichnen.
- In den aus der VA heraus ragenden Kegelteil etwa 5 Schnittebenen 1 - 5 einzeichnen. Sie ergeben kreisförmige Ebenen.
- Die Schnittebenen in die DS projizieren.
- In der DS die Kreise 1 - 5 zeichnen. Sie ergeben mit der vorderen Kerzenwand jeweils einen Schnittpunkt S1D bis S5D.
- S1 bis S5 in die VA projizieren (ergibt Punkte S1V bis S5V).
- S1V bis S5V verbinden: Man erhält die Durchschmelzkurve ( = Durchdringungskurve).