Kugelförmige Werkstücke: Darstellung, Bemaßung, Durchdringung 19.07.2010, 16:12

Für das Zeichnen von Kugeln sieht die Zeichnungsnormung besondere Darstellungs- und Bemaßungsregeln vor. Sie werden hier zusammen mit der Konstruktion von Kugeldurchdringungen gezeigt. Mit zwei Aufgaben zum Üben.

Kugelförmige Werkstücke

Darstellung

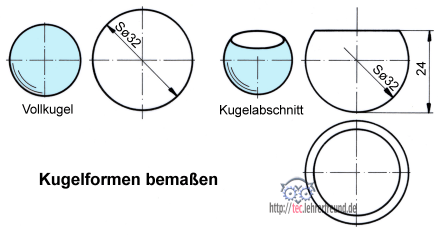
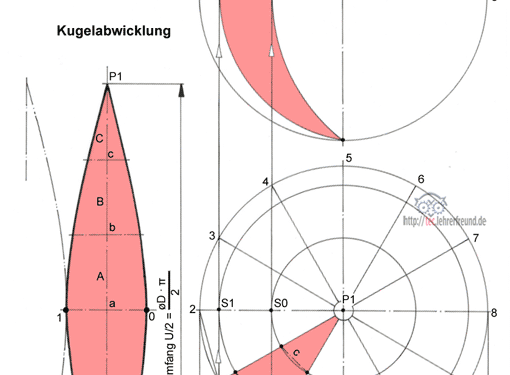
Für die Darstellung der Vollkugel genügt eine Ansicht, bei Kugelabschnitten sind für ein eindeutiges Erkennen zwei Ansichten erforderlich.

Bemaßung

Kugelformen bemaßen

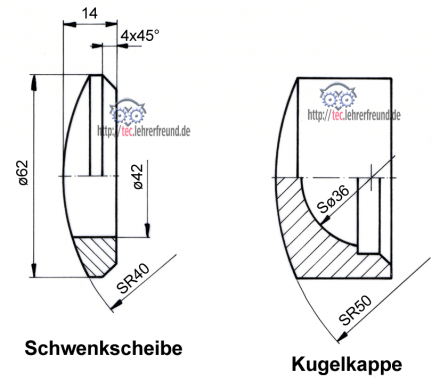
Der Großbuchstabe S (= Sphäre) ist das Symbol für die Kugelform. Nach DIN 406-1 steht S vor dem ø-Symbol oder vor dem Großbuchstaben R (= Radius) sowie der Maßzahl (hier die Maße Sø36 und SR50).

Ist der Kugelmittelpunkt angegeben, dann muss vor dem Kugelmaß das ø-Symbol eingetragen werden. Wird der Kugelmittelpunkt nicht gezeichnet, dann steht anstelle des ø-Symbols der Großbuchstabe R für den Kugelradius.

Kugeldurchdringungen

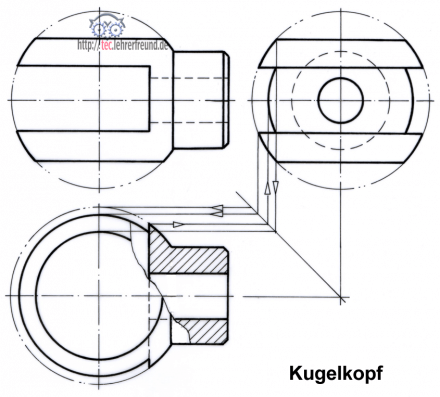
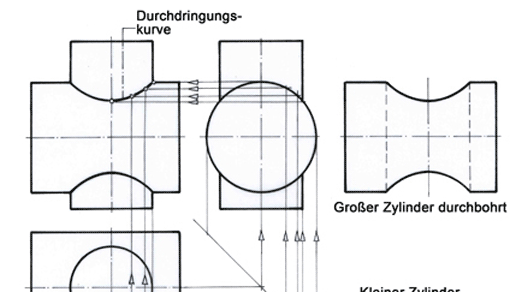
Kugelkopf in drei Ansichten

Durchdringt ein Zylinder oder ein Kegel eine Kugel mittig, dann entsteht als Durchdringungskurve in der Vorderansicht eine Gerade. Im Bauteil »Kugelkopf« ist es der rechts anschließende zylindrische Hals, der mit einer Geraden auf die Kugelform stößt. Die Abflachung der Kugel und der mittige Schlitz führen in der Draufsicht zu kreisförmigen Begrenzungen.

Die äußeren Kugelformen der Schwenkscheibe und der Kugelkappe werden ebenfalls von Zylindern begrenzt, weshalb gerade Durchdringungslinien entstehen.
 

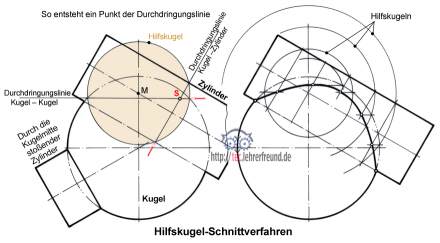
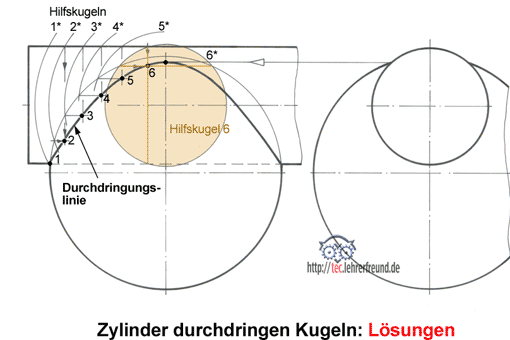
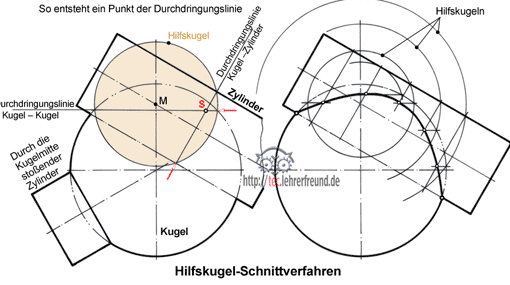
Das Hilfskugel-Schnittverfahren

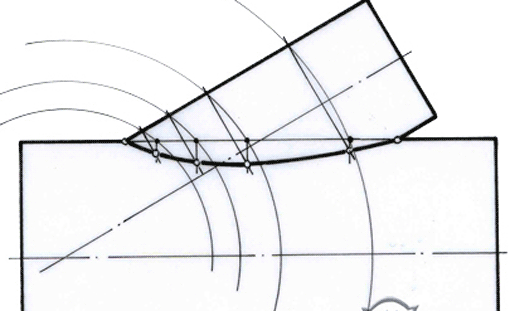
Bei der Konstruktion von Durchdringungskurven arbeitet man üblicherweise mit sinnvoll ausgewählten Schnittebenen. Die Schnittpunkte, die man dabei in einer Ansicht erhält, projiziert man in die weiteren Ansichten.
Das Hilfskugel-Schnittverfahren hat den Vorteil, dass man mit einer einzigen Ansicht auskommt; an das Raumvorstellungsvermögen des Zeichners stellt es aber einige Anforderungen. Das Verfahren eignet sich nur bei Formen, die sich mittig durchdringen. Im gezeigten Beispiel stößt ein Zylinder mittig und schräg durch eine Kugel.

So geht man vor: Man zeichnet die Ansicht, in der die Durchdringungslinie sichtbar ist. Um den Mittelpunkt M von Kugel- und Zylinderachse zieht man Hilfskugeln, die als Kreise erscheinen. Dabei bildet jede Hilfskugel beim Durchstoßen der Kugel und des Zylinders verschieden große Kreisflächen. Der Schnittpunkt je zweier dieser Flächen erzeugt einen Punkt der Durchdringungskurve. Die linke Darstellung zeigt die Konstruktion eines solchen Schnittpunkts (S). In der rechten Zeichnung wird mit vier Hilfskugeln gearbeitet. Zu beachten: Legt man die Hilfskugeln zu eng nebeneinander, dann erhält man zu viele (verwirrende) Schnittpunkte.

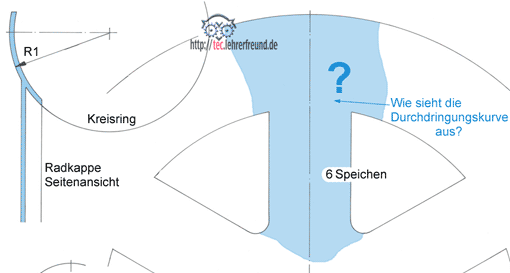
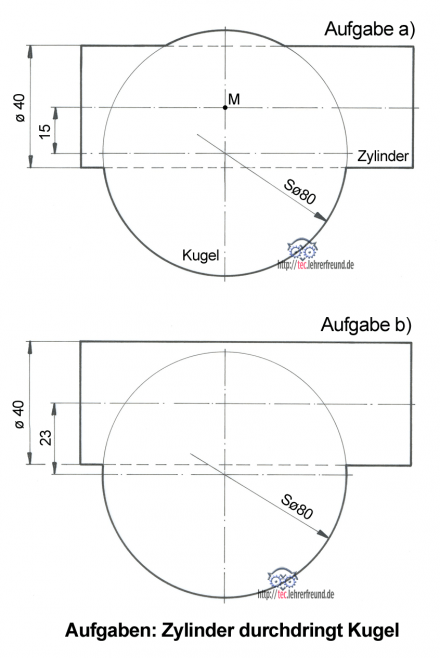
Zwei Aufgaben:

Zeichnen Sie die beiden folgenden Übungen im Maßstab 1:1 und konstruieren Sie die Durchdringungskurven mit dem Hilfskugel-Verfahren. Legen Sie die Hilfskugeln in den Punkt M. Die Lösung finden Sie im nächsten Beitrag.

Weitere Themen im tec.LEHRERFREUND zur Zeichnungsnormung:

- Kegelformen
- Toleranzen
- Werkstückoberflächen
- Bemaßungsregeln
- Ansichten darstellen

und weitere.