Berechnung gestreckter Längen 19.11.2010, 09:34
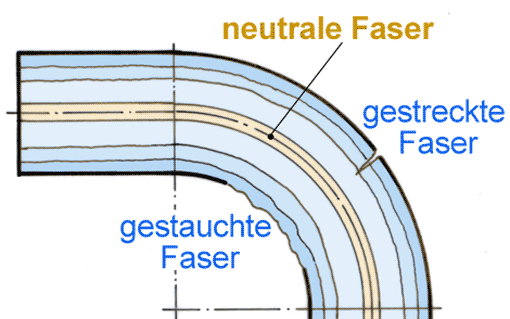
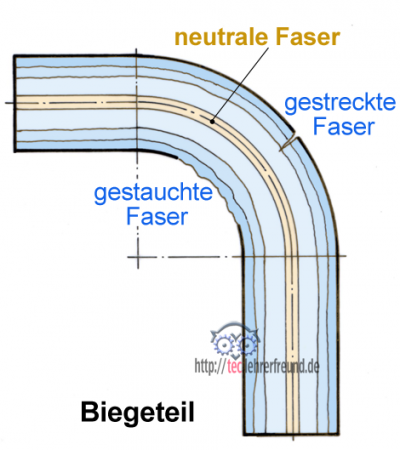
Vor der Herstellung eines Biegeteils muss man seine »gestreckte« Länge kennen. Sie wird über die neutrale Faser ermittelt. Handelt es sich um einen geraden Stab mit rechteckigem, rundem oder sonstwie symmetrischem Querschnitt, dann liegt die neutrale Faser in Querschnittmitte. Bei anderen Querschnittsformen ist zuerst die Lage der neutralen Faser zu bestimmen.
1. Ausbildungsjahr
Gestreckte Längen berechnen
Vor der Herstellung von Biegeteilen ist deren »gestreckte« Länge L zu berechnen. Sie ist die abzusägende Länge und entspricht der neutralen Faser des Teils. Die neutrale Faser liegt bei symmetrischen Querschnitten (runder, rechteckiger Querschnitt) genau in der Mitte zwischen dem äußeren und dem inneren Biegeradius. Bei sehr kleinen Biegeradien muss die Berechnung mit einem Ausgleichsfaktor (siehe weiter unten) durchgeführt werden.
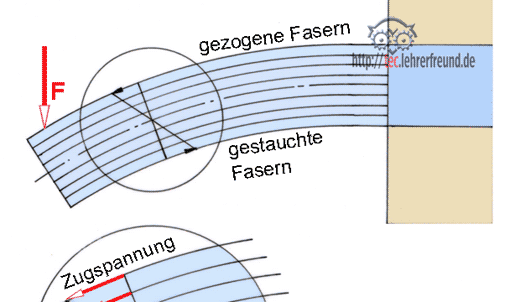
Als neutrale Faser bezeichnet man in der technischen Mechanik die Linie eines Biegequerschnitts, deren Länge sich bei einem Biegevorgang nicht ändert. Die weiter außen liegenden Fasern werden beim Biegen gedehnt die weiter innen liegenden gestaucht. Für die gedehnten Fasern besteht die Gefahr der Entstehung von Biegerissen durch Überbeanspruchung des Werkstücks oder wenn der Biegeradius zu klein ist.
Beim Begriff »Faser« lehnt man sich an die Vorstellung an, dass das Material in einzelnen Schichten aufgebaut ist, so wie sie in mehreren Walzvorgängen tatsächlich entstehen.
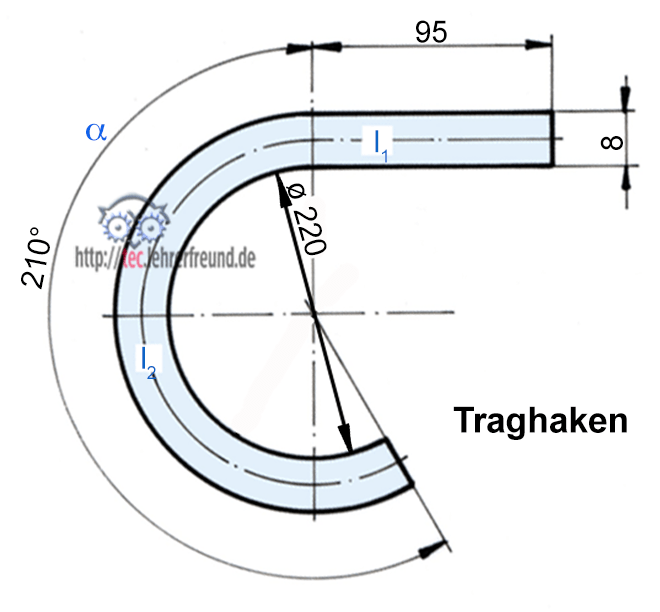
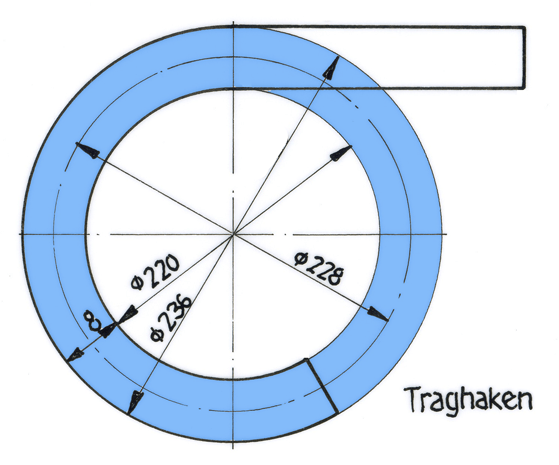
Berechnungsbeispiel Traghaken, Flachstahl 8 x 12
Die gestreckte Länge ist zu berechnen.
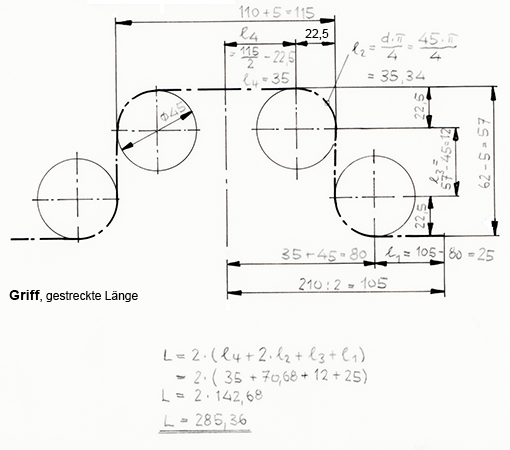
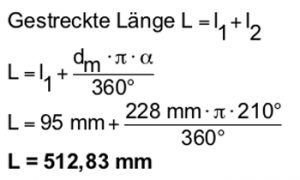
Der Traghaken besteht aus einem geraden Teilstück l1 und einem offenen Kreisbogen l2. Beim Berechnen des Kreisbogens muss die neutrale Faser in der Querschnittmitte verwendet werden: dm = 220 mm + 2 • 4 mm = 228 mm.
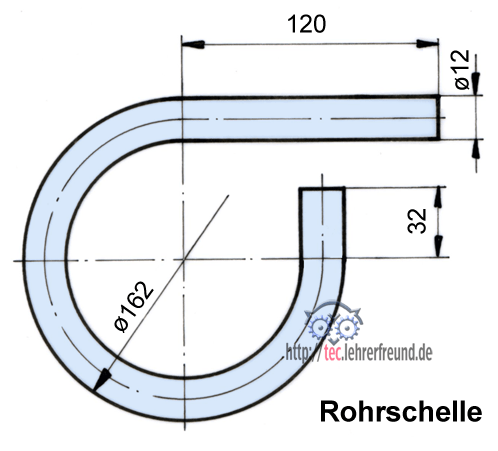
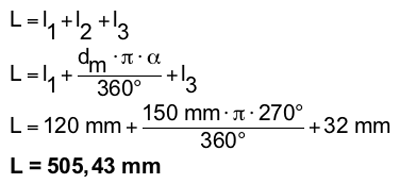
Berechnungsbeispiel Rohrschelle, Rundstahl ø12
Die gestreckte Länge ist zu berechnen.
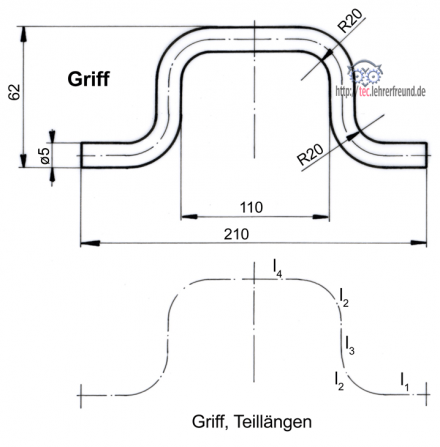
Berechnungsbeispiel Griff, Rundstahl ø5
Die gestreckte Länge ist zu berechnen.
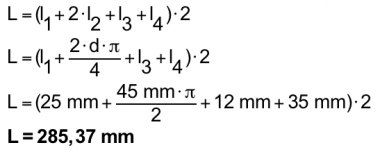
Kleine Biegeradien
Bei Biegeradien, deren Radius R kleiner als 5 mal Blechdicke (R < 5 • s) ist, verschiebt sich durch zusätzliche Materialverformungen die neutrale Faser. Dann muss die Länge der neutralen Faser berichtigt werden. Der Ausgleichswert dafür ist v; man findet ihn in Tabellen. Bei 90°-Biegewinkeln wird dann folgende Formel angewendet:
L = l1 + l2 + l3 + ... – n • v (n = Anzahl der Biegestellen am Werkstück)
Tabelle Ausgleichswerte:
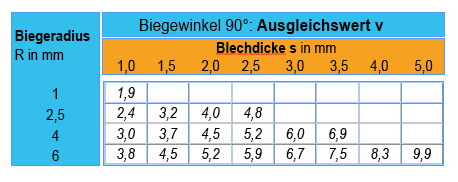
Berechnungsbeispiel Griff (oben) mit auf R = 6 mm verringerten Radien, vier Biegestellen:
L = (l1 + 2 • l2 + l3 + l4) • 2 – 4 • v
L = (l1 + 2 • d • 3,14 : 4 + l3 + l4) • 2 – 4 • v
L = 39 mm + 17 mm • 3,14 : 2 + 40 + 49) • 2 – 4 • 9,9 =
L = 269,8 mm
___________________________
Ergänzung Kommentar sts
Ergänzung Kommentar Taeb