Drehmomente (3): Seilwinde 12.04.2010, 13:13

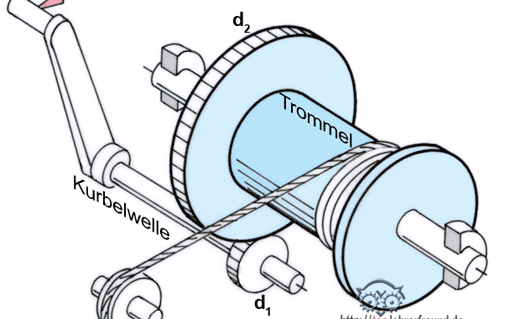
Wie Drehmomente an einer Seilwinde wirken. Berechnungsbeispiel zur Ermittlung der Windenlast, mit methodischen Anregungen für den Unterricht.

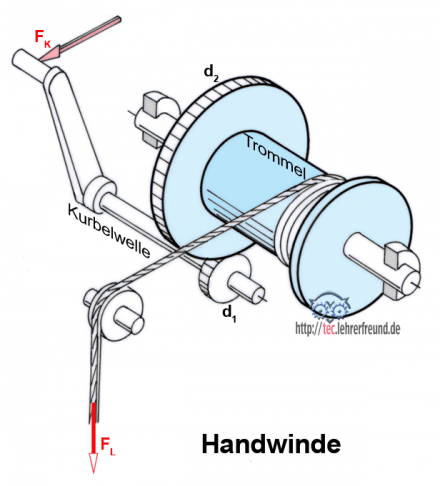
Drehmomentberechnung an einer Handwinde 

Aufgaben: 

– Welche Übersetzung hat das Zahnradgetriebe?

– Wie viele Umdrehungen macht die Handkurbel bei 1 Trommelumdrehung?

– Welches Drehmoment entsteht an der Trommel?

– Welche Last F_L wird mit der Seilwinde bei einer Handkraft F_K = 150 N gehoben?

Methodische Hinweise

Die Wirkungsweise der Seilwinde erschließt sich im Unterricht nicht dadurch, dass man sich gewissermaßen hinter Formeln verschanzt und wild darauf losrechnet. Man muss mit den Schülern zuvor dies erarbeiten: Die Winde besteht aus zwei starren Systemen, deren Nahtstelle der Zahnradtrieb ist. Dort wird das über die Handkurbel eingeleitete Drehmoment mit der Kraft F_z1 an das Trommelsystem weitergegeben und das Drehmoment gleichzeitig vergrößert.
Im Einzelnen: Das Drehmoment F_K ∙ r_K wirkt - weil die Gesamtkurbel starr ist - auch am Ritzel d₁, also:
F_z1 ∙ r_z1 = F_K ∙ r_K

Dabei muss, entsprechend dem kleineren Hebelarm am Ritzel, F_z1 größer sein als F_K. Am großen Trommelzahnrad d_z2 ist also F_z2 = F_z1. Das neue Drehmoment F_z2 ∙ r_z2 wirkt auch an der Seiltrommel. Weil deren Durchmesser kleiner ist als d₂, wird die Trommelkraft (= Seilzugkraft) ein weiteres Mal vergrößert. 
Auch dies sollte geklärt werden: Ein Wirkungsgrad η = 0,65 = 65% bedeutet, dass innerhalb der Hubwindenmechanik mehr als ein Drittel der eingesetzten Energie durch Reibungsverluste verloren geht. Dies hat zur Folge, dass weniger Last gehoben werden kann als theoretisch möglich.

Lösung der Aufgaben

Bekannte Größen:

Handkraft F_K= 150 N

Radius der Handkurbel r_K = 360 mm

Trommeldurchmesser d_T = 200 mm

Teilkreis Trommelzahnrad d₂ = 460 mm

Antriebsrad d₁ = 64 mm

Gesamtwirkungsgrad η = 0,65

Erinnerung: Übersetzungen ändern in der Regel das Drehmoment von Welle zu Welle. Übersetzungen ins Langsame vergrößern das Drehmoment und umgekehrt.

Antrieb: Die Handkraft F_K soll in jeder Kurbelstellung senkrecht zur Handkurbel angreifen. Die Seildicke wird vernachlässigt.

Übersetzungsverhältnis des Zahnradgetriebes: 

i = d₂ : d₁ = 460 mm : 64 mm =

i = 7,188

Handkurbelumdrehungen bei 1 Trommelumdrehung (n_T = 1):

i = n_K : n_T   –> n_K = i ∙ n_T = 7,188 ∙ 1 Umdrehung

n_K = 7,188 Umdrehungen

Drehmoment an der Trommel: 

i = M₂ : (M₁ ∙ η)  = M_Trommel : (M_Kurbel ∙ η)

M_Trommel  = M_K ∙ i ∙ η = F_K ∙ r_K ∙ i ∙ η

M_Trommel  = 150 N ∙ 0,360 m ∙ 7,188 ∙ 0,65 =

M_Trommel  = 252,28 Nm

Hublast: 

Aus M_Trommel  =  F_L ∙ d_T / 2  –> F_L = 2 ∙ M_T : d_T

F_L = 2 ∙ 252,28 Nm : 0,2 m =

F_L = 2 523 N 

________________________

Informationen zum Thema in:
Hebel und Drehmoment
Zahnradberechnung