Hebebühne (2): Kräfte am Scherenhebel 13.04.2015, 06:12
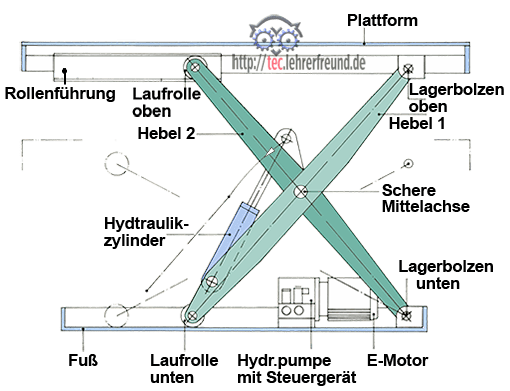
Im Beitrag »Hebebühne (1): Scherenbühne« stellten wir die Scherenbühne mit ihren Einzelteilen vor und animierten den Leser, den Hebel 2 freizumachen. Hier wird ein Lösungsvorschlag mit der Berechnung der Kräfte gezeigt.
Scherenbühne, Kräfte am Scherenhebel
Vor der Berechnung des Hebels Pos. 2 stellen wir einen ähnlichen Fall vor und rechnen ihn durch, um warmzulaufen.
Hubwagen
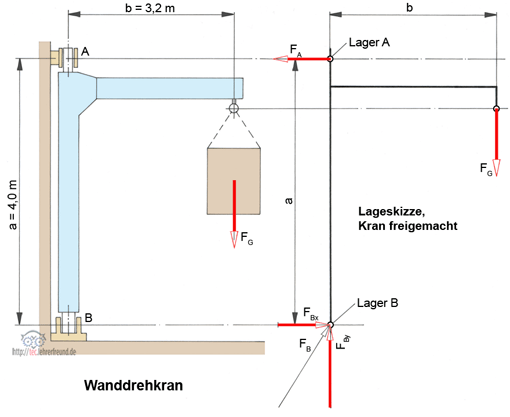
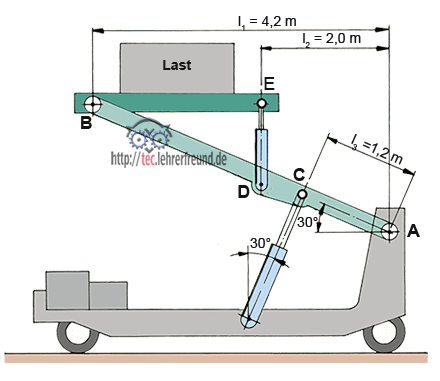
Der hier dargestellte Hubwagen war vor Jahren eine Statik-Prüfungsaufgabe in einem Techn. Gymnasium. Sie ist leichter zu bewältigen als unsere Scherenbühne, denn der Erfinder der Aufgabe sorgte zur Freude der Prüflinge dafür, dass außer der Last FB auch die Zylinderkraft FD senkrecht wirkt. (Dies würde sich sofort ändern, wenn die Last nach oben gefahren würde: Der Zylinder würde sich schräg nach links stellen. In der neuen Position wäre die Aufgabe unlösbar – ebenso wie unsere Scherenhebel-Aufgabe.
Die Last steht mittig auf der Plattform, so dass B und D gleich stark belastet werden. Bekannt sind also die auf die Punkte B und D wirkenden Kräfte: FB = FD = 750 daN. α = 30°. Unbekannt sind FC und FA. Sie wollen wir berechnen.
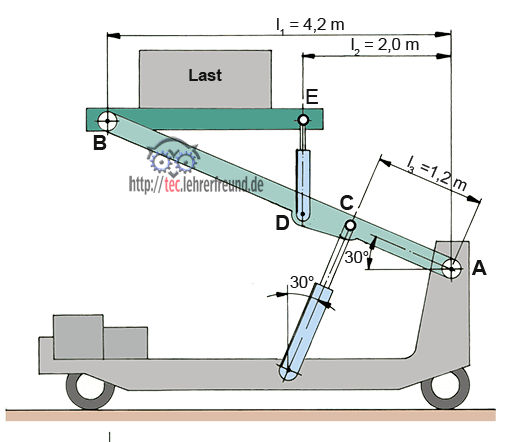
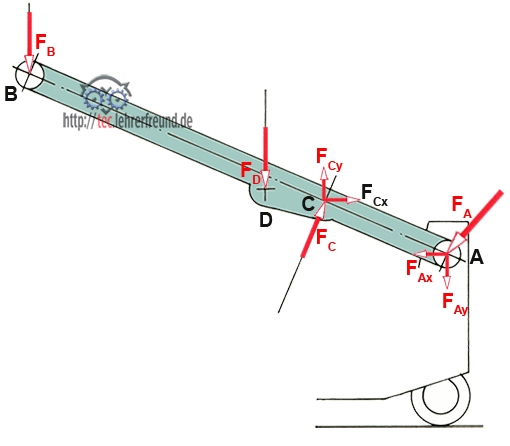
Bild unten: Ausleger freigemacht
Wir stellen die drei Gleichgewichtsbedingungen auf:
ΣMA = 0 = FB • l1 + FD • l2 – FC • l3. Wir stellen die Gleichung nach FC um:
FC = (FB • l1 + FD • l2) : l3. Wenn wir die Zahlen einsetzen, ergibt sich für
FC = 3 875 daN
ΣFX = 0 = FCx – FAx ––> FAx = FCx
FAx = FCx = FC • sin α = 3 875 daN • 0,5 =
FAx = 1938 daN = FCx
ΣFY = 0 = FB +FD – FCy + FAy
FAy = FCy – FB – FD
cos α = FCy : FC ––> FCy = FC • cos α = 3875 daN • 0,866
FCy = 3 356 daN
FAy = 3 356 daN – 750 daN – 750 daN
FAy = 1 856 daN
FAx = FCx = FC • sin α = 3875 daN • 0,5
FAx = 1 938 daN
FA = √ (FAx daN)2 + FAy daN)2
FA = 2683 daN ––> tan β = FAx : FAy = 1 938 daN : 1 856 daN = 1,044 ––> β = 46,2° (zwischen FA und der Senkrechten)
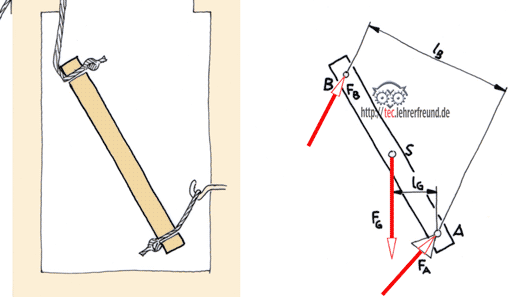
Wir kommen zur Scherenbühne und zum Hebel 2 zurück.
Unten: Der freigemachte Hebel 2.
Gegeben:
FL = 6 000 N
l = 1300 mm
lK = 715 mm
l3 = 645,2 mm
α = 52°; β = 27°.
Zu berechnen sind:
a) Abstand a
b) Abstand b
c) Kraft F3
d) Mit Hilfe der Gleichgewichtsbedingungen berechnen: Die Kräfte FK, F3 und FA mit ihren horizontalen und vertikalen Komponenten FKx, FKy, F3x, F3y, FAx und FAY.
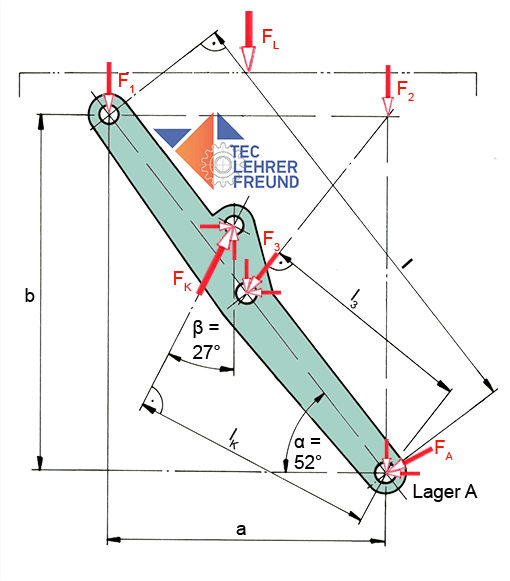
Bild unten: Hilfsskizzen für die Verwendung von Winkelfunktionen

Lösungsvorschläge:
a) (Skizze Dr1): cos α = a : l –> a = l • cos α = 1300 N • 0,6157 =
a = 800,4 N
b) sin α = b : l –> b = l • sin α =1300 N • 0,788 =
b = 1 024,4 N
c) (Skizze Dr2) F3: sin α = F2 : F3 –> F3 = F2 : sin α = 1 500 N : 0,788 =
F3 = 1 903,5 N
d) Gleichgewichtsbedingungen:
ΣMA = 0 = F1 • a – FK • lK + F3 • l3 –> FK = (F1 • a + F3 • l3) : lK =
FK = 3 397 N
ΣFX = 0 = FKX – F3X – FAX –> FAX = FKX – F3X
(Skizze Dr3): FKX: sin β = FKX : FK –> FKX = FK • sin β = 3 397 N • 0,454 =
FKX = 1 542 N
(Skizze Dr2) F3X: cos α = F3X : F3 –> F3X = F3 • cos α = 1 903,5 N • 0,6157 =
F3X = 1 172 N
FAX = 1 542 N – 1 172 N =
FAX = 370 N
ΣFY = 0 = F1 – FKY + F3Y + FAY –> FAY = FKY – F1 – F3Y
(Skizze Dr3) FKY: cos β = FKY : FK –> FKY = FK • cos β = 3 397 N • 0,891 =
FKY = 3 027 N
(Skizze Dr2) F3Y: sin α = F3Y : F3 –> F3Y = F3 • sin α = 1 903,5 N • 0,788 =
F3Y = 1 500 N ( = F2)
FAY = 3 027 N – 1 500 N – 1 500 N = 27 N
FAX = 370 N
tan γ = FAY : FAX = 27 N : 370 N = 0,073 –> γ = 4°23'
sin γ = FAY : FA –> FA = FAY : sin γ = 27 N : 0,076 =
FA = 355 N
FA wirkt mit 355 N unter dem Winkel γ = 4° 23' zur Waagrechten (siehe Skizze freigemachter Hebel 2).