Bauteilbelastungen: Die richtigen Kräfte aufspüren (2) 23.03.2015, 06:59
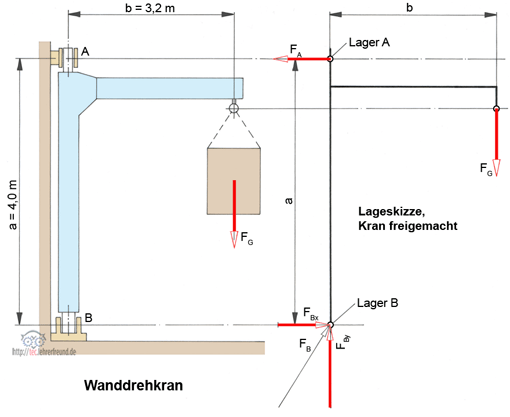
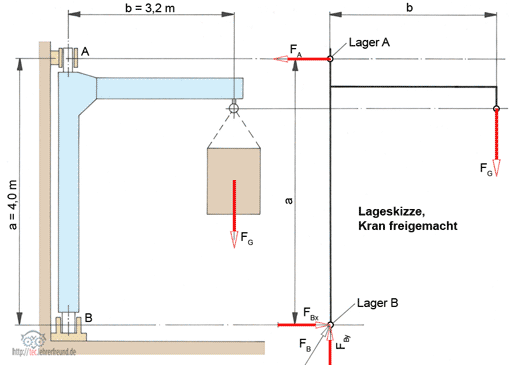
Das Freimachen beginnt man mit einer Lageskizze, die auf einen Blick zeigt, ob eine Aufgabe richtig angepackt wurde. Die Lageskizze ist eine Reduktion auf das Wesentliche der Aufgabe.
Im Beitrag »Die richtigen Kräfte aufspüren (1)« zeigten wir im Überblick, wie man an Statikaufgaben herangeht, die auf der Ebene Technischer Gymnasien verlangt werden, und wiesen auf einige Vereinfachungen hin. Im folgenden finden Sie praktische Beispiele dazu.
Wahl einer geeigneten Baugruppe
Alle Kräfte zu kennen, die innerhalb eines Systems wirken, ist nicht nötig. Beispiel Radfahrer: An dem hier gezeigten System wirken mindestens 14 Kräfte. Das Gesamtrad drückt an beiden Reifenaufstandspunkten gegen die Straße, die ihrerseits dagegen hält. Die Hände drücken gegen den Lenker, dessen Reaktionskraft wir nach längerem Fahren schmerzhaft spüren. Dasselbe zwischen Gesäß und Sattel, zwischen Fußsohle und Pedal. Zwei weitere Gegensatzpaare sind Antriebskraft und Reibung, die Erde zieht am System Rad und Fahrer.
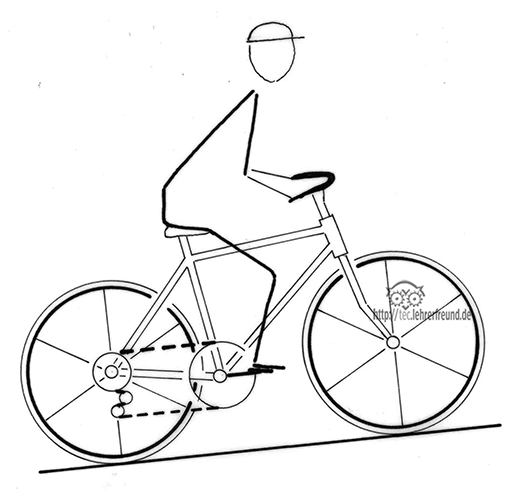
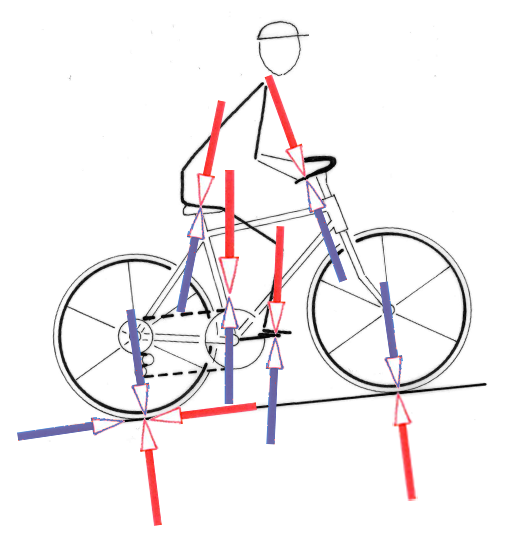
Newtons Erkenntnis actio = reactio bedeutet, dass Kräfte immer in Paaren auftreten, die sich gegenseitig aufheben. Durch das Freimachen werden diese Nullsummen-Kräftepaare aufgetrennt, sodass eine Berechnung leichter möglich wird. Aufgetrennt wird zwischen den Kräftepaaren, die zwischen der gewählten Baugruppe und dem Rest des Systems wirken, Kräftepaare innerhalb oder außerhalb der Baugruppe bleiben unberücksichtigt, denn sie heben sich ja auf.
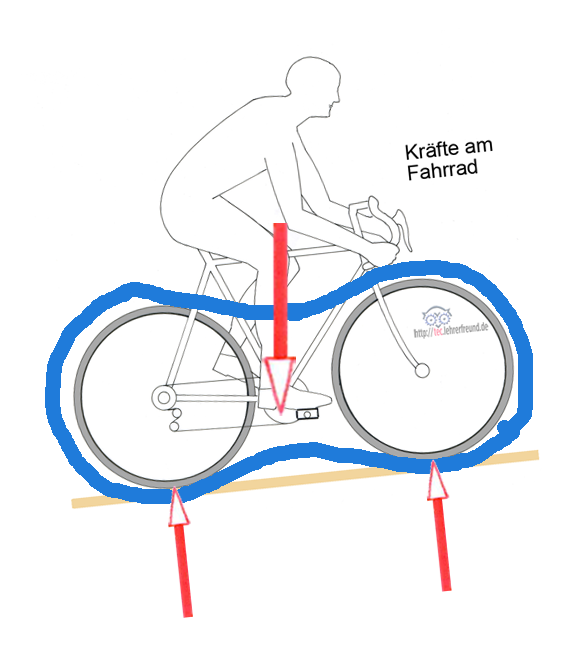
Wir sollen beispielsweise nur die Radaufstandskräfte ermitteln. Wie gehen wir vor?
Wir kreisen die uns interessierende Baugruppe ein (Skizze, blaue Umrahmung). Das führt dazu, dass wir alle Kräftepaare, die innerhalb oder außerhalb des Kreises liegen, ignorieren. Von den Kräftepaaren, die an der Grenze der Baugruppe liegen bzw. von der Systemgrenze zerschnitten werden, betrachten wir nur die Kräfte, die von außen auf die Baugruppe wirken.
Meint man aber, die Zahl der unbekannten Kräfte überstiege die der lösbaren, muss man untersuchen, ob es vielleicht übersehene Informationen gibt. Wenn nicht, ist es vergeblich, nach einer weiteren Lösung zu suchen.
Allgemein ist eine Baugruppe geeignet, wenn
– die Kräfte, die wir berechnen wollen, auf sie wirken,
– es mindestens eine bekannte Kraft gibt (sonst finden wir keine Lösung),
– höchstens drei unbekannte Größen mit ihren Beträgen und/oder Richtungen vorhanden sind, denn drei Gleichgewichtsbedingungen lassen die Lösung von nicht mehr als drei Unbekannten zu.
Lageskizze
Wir beginnen mit einer Lageskizze, die zeigt, welche Baugruppe freigemacht wurde. Eine Lageskizze ist eine unmaßstäbliche Skizze des Lageplanes. Die Lageskizze ist hilfreich, denn
– sie ist eine Reduktion auf das Wesentliche der Aufgabe. Sie zeigt, ob die Aufgabe verstanden wurde,
– sie zeigt, ob der Bearbeiter eine Baugruppe richtig freigemacht hat.
Bei rechnerischen Lösungen ist die Angabe der Kraftrichtungen wichtig, damit die Vorzeichen in den Gleichungen richtig sind. Werden bei zeichnerischen Lösungen die Kraftrichtungen nicht richtig angegeben, dann wird das Ergebnis negativ, was einfach bedeutet: Die Kraftrichtung wurde falsch gewählt.
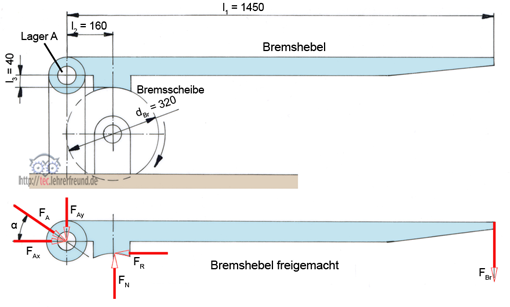
Beispiel Bremshebel:
Die Bremskraft FBr bewirkt eine senkrechte Druckkraft auf die Bremsscheibe. Beim Freimachen des Bremshebels wird die Reaktionskraft FN eingetragen. Dabei entsteht die waagrecht wirkende Bremskraft FR. Sie wirkt gegen die Drehrichtung der Bremsscheibe. Das Lager A ist ein Festlager; die Lagerkraft FA wird in die Komponenten FAx und FAy zerlegt.
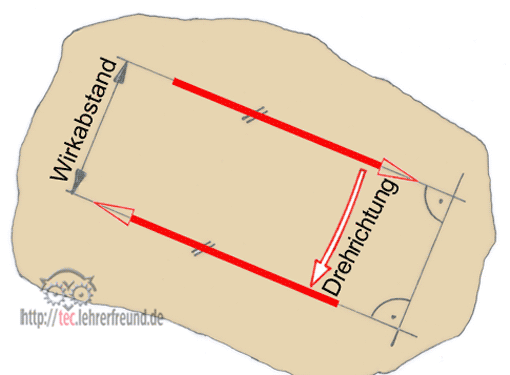
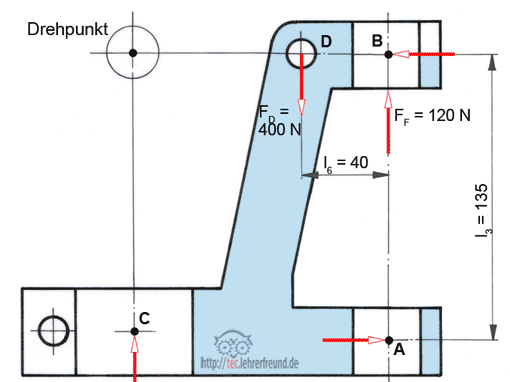
Beispiel Führungsgabel:
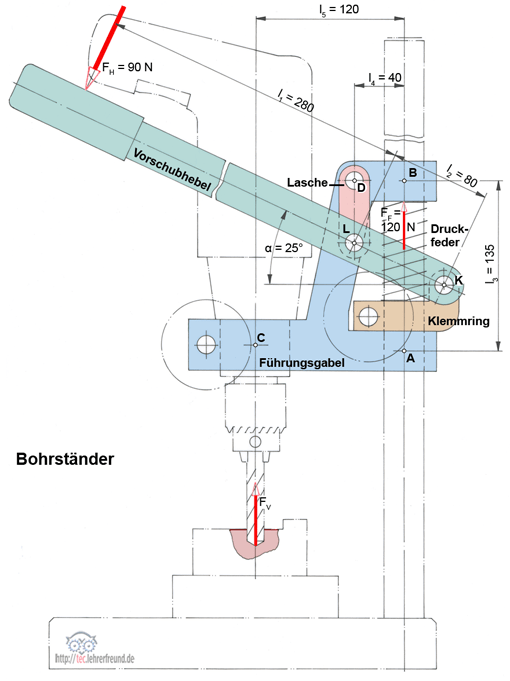
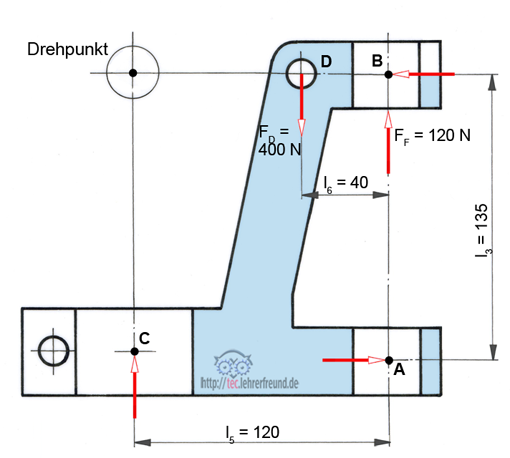
Die Laschenachse drückt mit FD senkrecht nach unten. Die Gegenkraft ist die vom Werkstück herkommende Kraft FC. Sie erzeugt ein rechtsdrehendes Moment, auf das die Maschinensäule mit einem linksdrehenden Moment reagiert. Dabei entstehen die waagrechten Kräfte FA und FD. Die Feder drückt mit FF senkrecht nach oben.
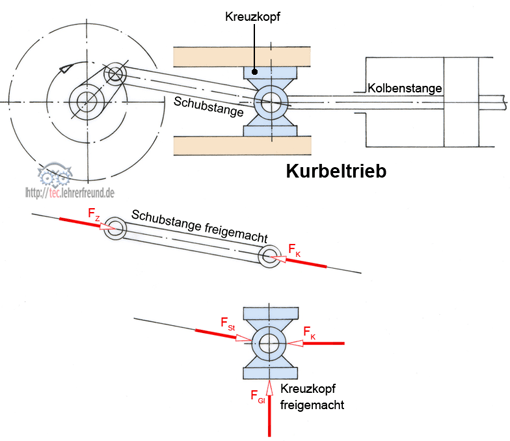
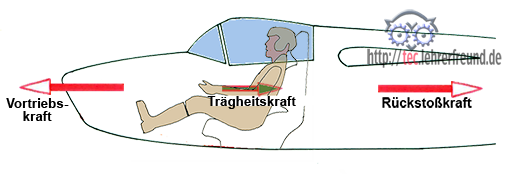
Körper in Bewegung
Will man einen bewegten Körper beschleunigen oder abbremsen, benötigt man eine Kraft, d. h.: Körper setzen einer Bewegungsänderung einen Widerstand entgegen, die Trägheitskraft FT. Massen wehren sich gewissermaßen dagegen, dass sie beschleunigt oder gebremst werden sollen; sie wollen in ihrer Lage verharren.
Nähres dazu erfahren Sie in »Dynamik (1)«