Bauteilbelastungen: Die richtigen Kräfte aufspüren (1) 14.03.2015, 06:00

Ein Überblick, was beim Freimachen von Bauteilen zu beachten ist.

Wo die Last drückt

Dieser Überblick zeigt, wie man an Statikaufgaben herangeht, die auf der Ebene Technischer Gymnasien verlangt werden. Hier gelten gegenüber der auf Universitätsebene betriebenen Statik folgende Vereinfachungen:

– Alle Körper werden als starr angenommen, so dass Verformungen unberücksichtigt bleiben.
– Reibungswiderstände werden in der Regel vernachlässigt, es sei denn, man würde ihre Berechnung ausdrücklich fordern. 
– Man beschränkt sich auf in der Ebene liegende Situationen. Dadurch reduziert sich die Anzahl der Gleichgewichtsbedingungen auf drei: ∑Fx = O; ∑Fy = O; ∑M = O.
– Die betrachteten Kräfte wirken immer nur an einem Punkt.

Einen Körper »freimachen« (auch »freischneiden«)

Voraussetzung für die Behandlung des Themas sind mathematische Grundkenntnisse: einfache Winkelfunktionen und das Aufstellen und Auflösen manchmal langer, aber einfacher Gleichungen. Beim Lösen statischer Aufgaben liegt die größte Hürde am Anfang des Lösungswegs, beim Freimachen/Freischneiden. Wurde richtig freigemacht, dann ist auch die richtige Lösung wahrscheinlich.

Bei der Lösung von Statikaufgaben geht man in drei Schritten vor:

1. Körper freimachen 
2. Lösungsverfahren wählen 
3. Lösen

Betrachtet man alle Kräfte, für die die Gleichgewichtsbedingungen der Statik gelten, dann sind dies solche, die von außen auf ein Bauteil oder eine Baugruppe wirken. Freimachen heißt also, von einem Bauteil oder einer Baugruppe alle angrenzenden Bauteile oder Baugruppen zu entfernen und durch Kräfte zu ersetzen. Kräfte wirken dort, wo Kontakte zwischen der gewählten Baugruppe und dem übrigen System bestehen. Ein Bauteil in diesem Sinne kann auch ein Mensch oder die Erde sein.

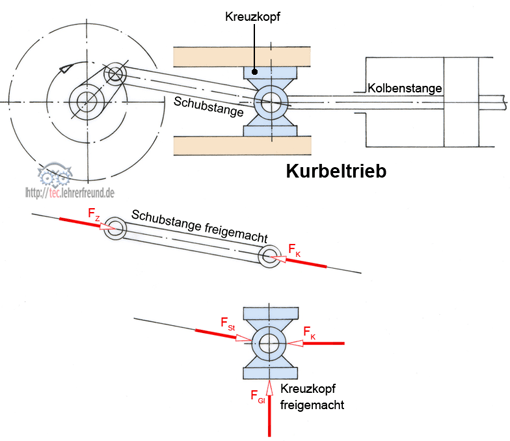
Beispiel: Kreuzkopf eines Kurbeltriebs 

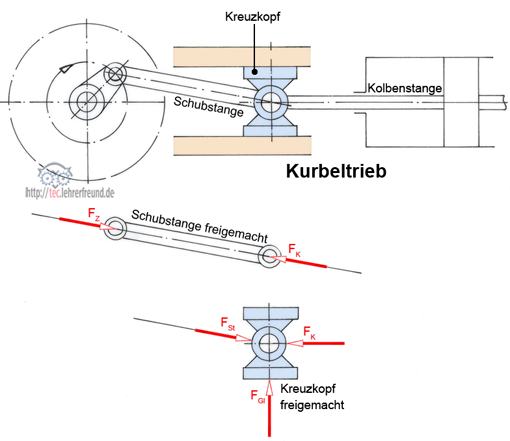
Der Kreuzkopf wird freigemacht, indem man die Schubstange wegnimmt und dafür die Kraft F_St (in Bezug auf den Kreuzkopf) einträgt. Dann ersetzt man die Kraftwirkung der Kolbenstange durch die Kraft F_K. Nun muss man noch die untere Gleitbahn vom Kreuzkopf wegnehmen. Dazu ist zu bemerken, dass zwischen reibungsfrei sich berührenden Flächen nur Normalkräfte, d. h. senkrecht zur Fläche wirkende Kräfte übertragen werden können (Bild). Eine Bewegungsprobe macht dies verständlicher: Verschiebt man die untere, geölte Gleitbahn waagrecht, wird der Kreuzkopf nicht mitgenommen, was bedeutet, dass die Gleitbahn keine Kraft auf den Kreuzkopf ausübt. 

Verschiebt man die Gleitbahn senkrecht, wird der Kreuzkopf angehoben (oder abgesenkt), also ist eine Kraftwirkung vorhanden. (Lesen Sie dies im Einzelnen nach unter »Kräfte ermitteln durch Freimachen«) 

Weiteres Beispiel für »Kräfte freimachen« 

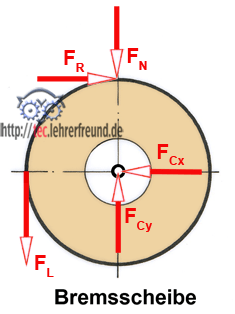
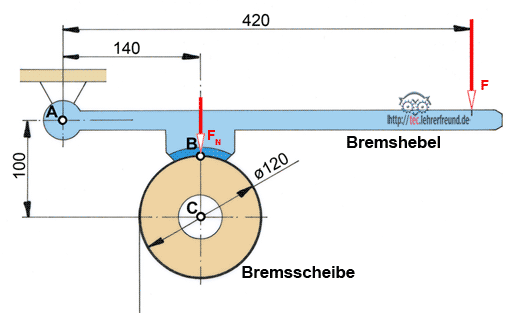
An der Backenbremse unten soll die Bremsscheibe freigemacht werden. Wir nehmen drei Teile weg und ersetzen sie durch Kräfte. Die drei Teile sind
– das Seil  
– der Bremshebel 
– Die Lagerachse C 

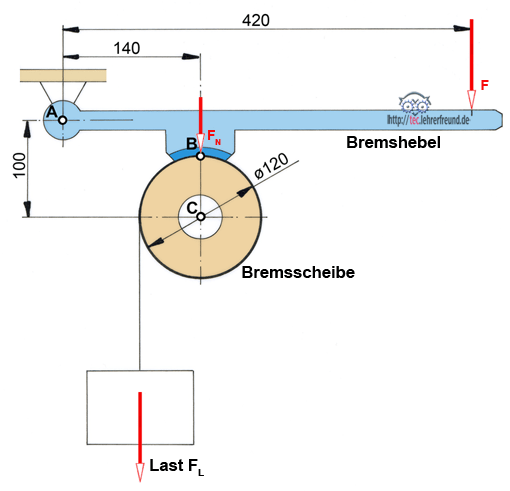
Bild unten:
Das Seil wird durch die Kraft F_L ersetzt. 
Der Bremshebel wird durch die Kraft F_N ersetzt. Außerdem muss eine Reibungskraft F_R eingesetzt werden. Sie wirkt gegen die Drehrichtung (linksdrehend) der Bremsscheibe.
Die Achse wird durch die Kraft F_C ersetzt. Weil man deren Richtung nicht kennt, zeichnet man statt F_C deren waagrechte und senkrechte Komponenten F_Cx und F_Cy.