Kreisanschlüsse 17.05.2008, 16:26
Formen darzustellen, in denen Geraden auf Kreise oder Kreise auf Kreise treffen, erfordern das Verständnis geometrischer Zeichentechniken. Wie findet man die genauen Anschlusspunkte? Sie finden hier die wichtigsten Kontruktionstechniken (Kreis + Gerade, Gerade berührt zwei ungleich große Kreise, Kreisbogen an zwei Kreise legen), außerdem einige Konstruktionsübungen.
Radiusdifferenzen und Tangenten
Immer wieder haben wir mit Formen zu tun, in denen Geraden auf Kreise oder Kreise auf Kreise treffen. Dies ist der Fall bei einem Riementrieb, wo der Riemen auf den Scheibenumfang auf- oder abläuft. Eine nicht ganz leichte Aufgabe für Schüler besteht darin, die genauen Anschlusspunkte zu finden. Da muss man echte Geometrie betreiben.
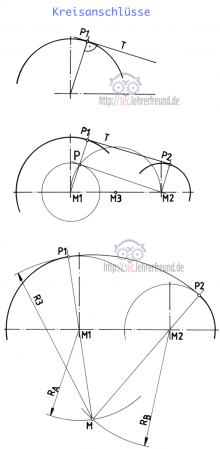
In der Zeichnung rechts finden wir folgende Situationen (Klick aufs Bild zum Vergrößern):
Kreis + Gerade (oben)
Den Anschlusspunkt P1 ermitteln wir, indem wir eine Senkrechte zur Tangente durch den Kreismittelpunkt ziehen.
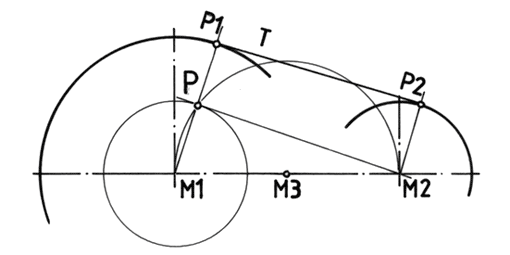
Gerade berührt zwei ungleich große Kreise (Mitte)
Schritte der Konstruktion:
- Wir tragen den kleinen Kreis 2 wird über der Mitte M1 des großen Kreises auf.
- Wir schlagen um M3 den Thaleskreis und erhalten so den Strahl M1 - P - P1.
- Diesen Strahl verschieben wir parallel in die Mitte M2 und erhalten P2.
Kreisbogen an zwei Kreise legen (unten)
Wir sollen den Kreisbogen mit Radius R3 exakt an die beiden Kreise 1 und 2 (Mitten M1 und M2) legen. Es könnte sich dabei um einen Nocken handeln.
Schritte der Konstruktion:
- Um M1 einen Kreisbogen mit RA = R3 minus R1 schlagen.
- Um M2 einen Kreisbogen mit RB = R3 minus R2 schlagen; Schnittpunkt M ist die Mitte von R3. Die Anschlusspunkte P1 und P2 ergeben sich als Schnittpunkte der verlängerten Strahlen M-M1 und M-M2.
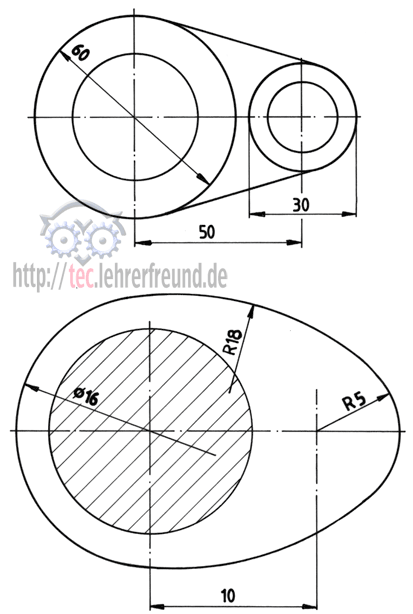
Konstruktionsübung:
Konstruieren Sie die beiden Teile unten, einen Hebel und einen Nocken, mit ihren Kreisanschlusspunkten.