Mountainbike 25.01.2012, 15:27
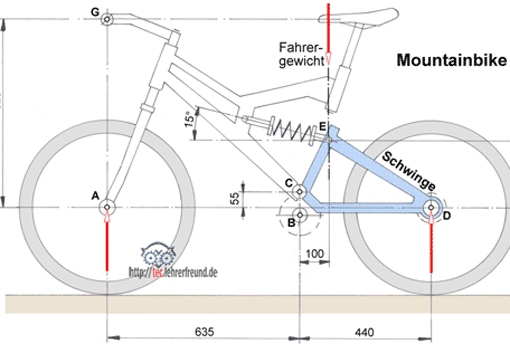
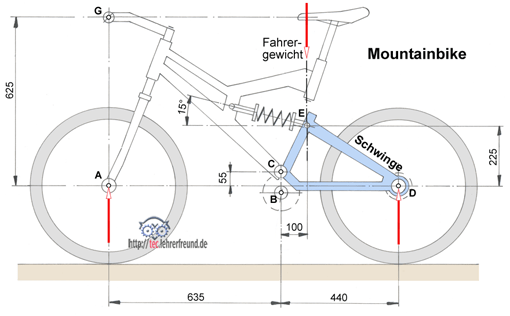
Manche Mountainbike-Modelle sind mit einer federnden Schwinge ausgestattet, die vom Boden herkommende harte Schläge dämpft. In diesem Beitrag werden die an der Schwinge angreifenden Kräfte und weitere Kräfte am Fahrrad ermittelt.
Lernniveau: Technische Oberschule, Berufskolleg u. Ä.
Mountainbike mit Federschwinge
Aus WIKI: »Ein Mountainbike (MTB) (engl. für Bergfahrrad) oder Gelände(fahr)rad ist ein Fahrrad, das besonders auf den Einsatz abseits befestigter Straßen ausgerichtet ist. Grundsätzlich ist das Geländerad ebenso wie das Rennrad eher Sportgerät als Verkehrsmittel, weshalb es üblicherweise nicht über die von der in Deutschland geltenden Straßenverkehrszulassungsordnung (StVZO) geforderte Ausstattung (Beleuchtung, Klingel und Rückstrahler) verfügt.«
Das Mountainbike ist mit einer federnden Schwinge ausgestattet, die vom Boden ausgehende harte Schläge dämpft. Die in der Skizze unten ins Fahrrad eingezeichneten Kräfte sind so zu verstehen: Der 750 N wiegende Biker sitzt auf dem Sattel und lässt sein Fahrrad - ohne zu treten - auf ebener Strecke auslaufen. C ist der Drehpunkt der Schwinge.
Aufgaben
1. Berechnen Sie die am Vorderrad angreifende Kraft FA und FD.
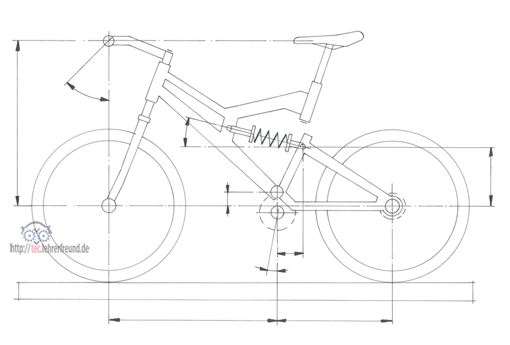
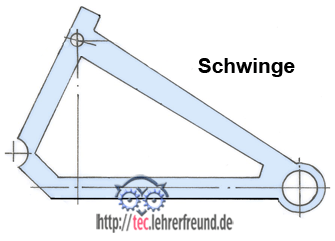
2. a) Zeichnen Sie die Schwinge als Einzelteil.
b) Zeichnen Sie die auf die Schwinge wirkenden Kräfte ein.
3. Die Federkraft FE ist zeichnerisch zu ermitteln.
4. Die Federkraft FE ist rechnerisch nachzuprüfen. Eine Differenz zur weniger genauen zeichnerischen Lösung von +/– 2% wäre zulässig.
Lösungsvorschläge
1. (Zeichnung unten) Drehpunkt bei FD angenommen.
Rechtsdrehendes Moment = linksdrehendes Moment:
FA · 1075 mm = FF · 440 mm –> FA = 750 N · 340 mm : 1075 mm
FA = 237,2 N
FD = FF – FA = 750 N – 237,2 N = 512,8 N
2 a. und 2 b.: Schwinge und Kräfte an der Schwinge:
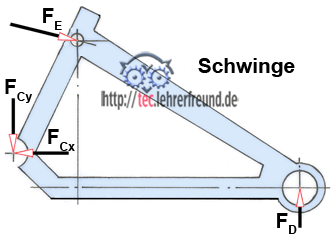
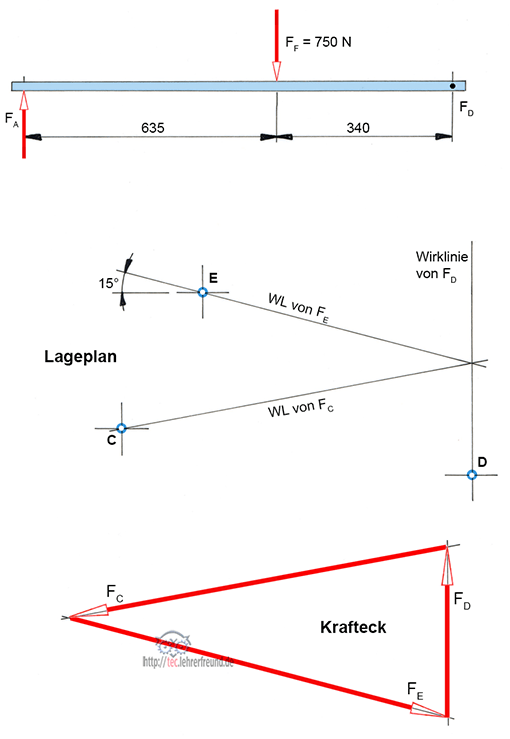
Beim Zeichnen des Kräfteplans werden die Kraftrichtungen aus dem Lageplan parallel in den Kräfteplan verschoben. Das Krafteck muss sich schließen.
FE herausgemessen: 1 200 N
3. Momentengleichung Σ M(C) = 0 = FD · 440 mm – FEx · 170 mm – FEy ·100 mm
FEx und FEy sind:
FEx = FE · cos 15°
FEy = FE · sin 15°.
Damit lässt sich die obige Momentengleichung schreiben:
FD • 440 mm = FEx · 170 mm + FEy · 100 mm, oder:
FD • 440 mm = FE · cos 15° · 170 mm + FE · sin 15° · 100 mm –>
FE • (cos 15° · 170 mm + sin 15° · 100 mm) = FD · 440 –>
FE = 1 187 N
(Die Differenz zur zeichnerischen Lösung 1 200 N beträgt etwa 1,1%)
___________________________
Die Skizze unten ist für die Verwendung in Arbeitsblättern gedacht.