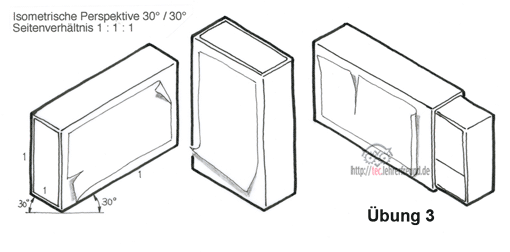
Perspektive-Kurs (3) 09.04.2014, 08:31
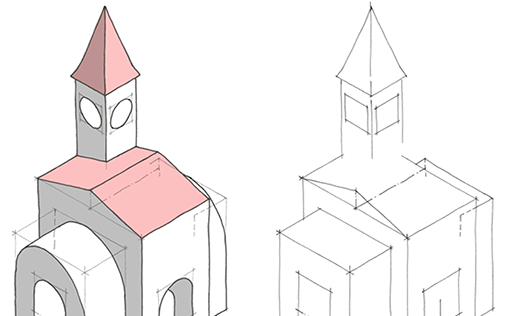
Kreise werden in der Perspektive immer zu Ellipsen. Beim Zeichnen einer Ellipse ist zu beachten, dass die großen und kleinen Bogen nahtlos ineinander übergehen. Mit einer Ellipsen-Näherungskonstruktion.
Perspektivisches Zeichnen
3. Der Kreis in der Perspektive
Kreise werden in der Perspektive immer zu Ellipsen (siehe Übungen 7 und 8). In der waagrecht liegenden Fläche liegt auch die Ellipse waagrecht. In senkrechten Flächen liegen die Ellipsen schräg. Beim Zeichnen der Ellipse ist zu beachten, dass die großen und kleinen Bogen nahtlos ineinander übergehen. Ellipsen mit Ecken gibt es nicht und seien die Ellipsen noch so flach.
Näherungskonstruktion
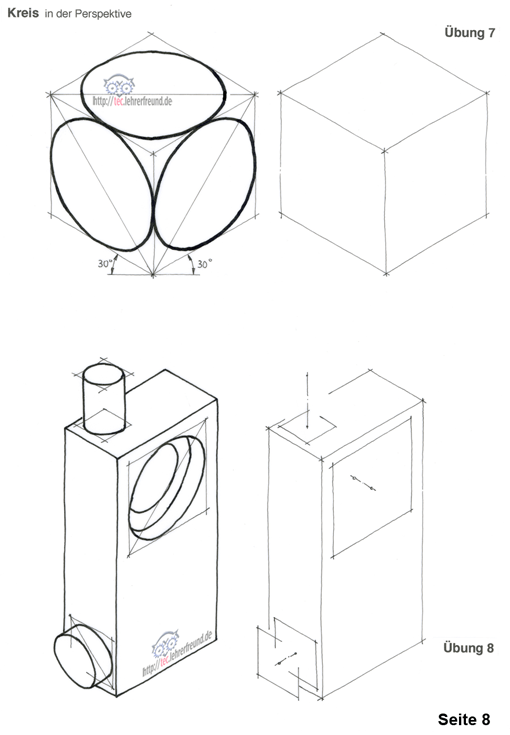
In ausreichender Näherung kann man eine 30°-Ellipse so konstruieren (Bilder unten):
- Raute mit Seitenlängen s (= Durchmesser) dünn vorzeichnen
- Von A und C aus Hilfslinie zum Schnittpunkt Mittellinie mit Rautenseiten ziehen
- In den Ecken A und C Zirkel einstechen und Radius R1 ziehen
- Kleinen Radius R2 von Schnittpunkt M1 (und M2) aus ziehen.
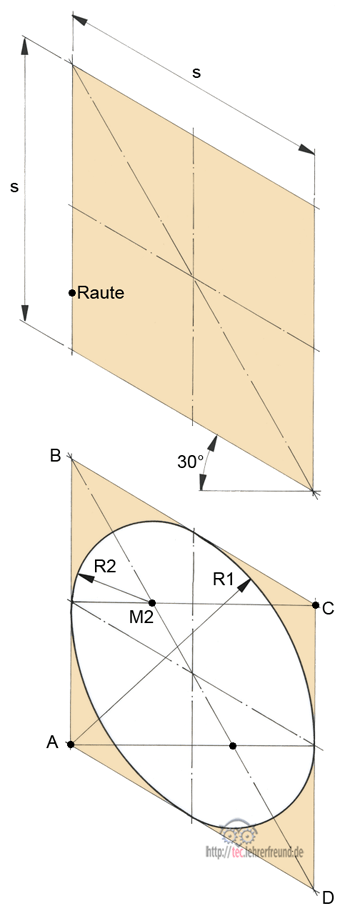
Um die richtige Größe der Ellipsen zu erhalten, zeichnet man zuerst die 30°-Raute vor, deren Ränder die Ellipse berührt. Die Kantenlängen der Raute entsprechen dem Durchmesser des Kreises, der als Ellipse gezeichnet wird: s = Kreisdurchmesser.
Übungen 7 und 8
Zeichnen Sie die Ellipsen wie in den beiden linken Skizzen vorgezeichnet.
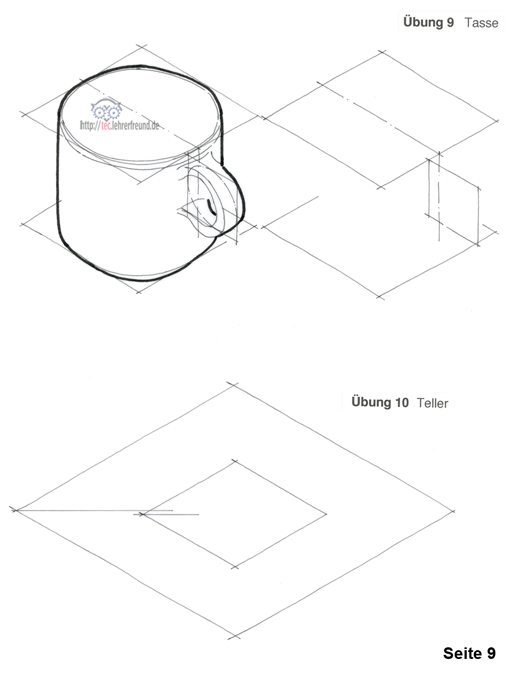
Übung 9
Eine Kaffeetasse mit Henkel ist zu zeichnen. Die Tasse ist in ihrer Grundform ein stehender Zylinder, der Henkel ein waagrecht liegender Ring. Benutzen Sie für die Übung die Vorzeichnungen rechts.
Übung 10
In dieser Übung soll die Tasse nochmals zusammen mit einer Untertasse gezeichnet werden. Wir geben eine Hilfestellung mit dem vorgezeichneten Umriss der Untertasse.
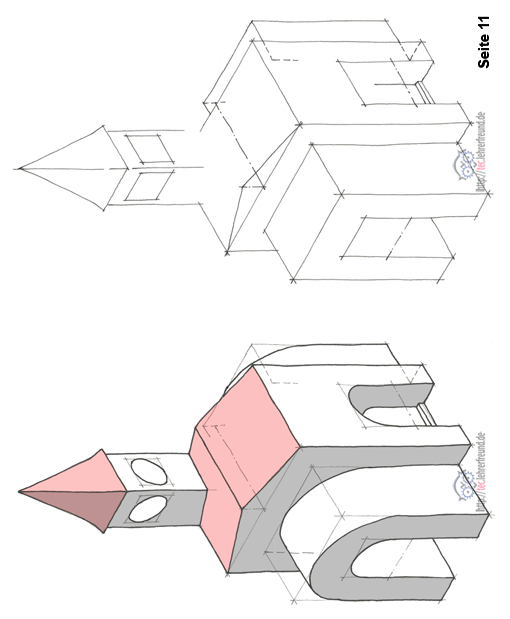
Übung 11