Lernprojekt Spannvorrichtung: Aufgaben (4) 31.07.2015, 05:35

Das Lern- und Übungsprojekt »Spannvorrichtung« wird in diesem Beitrag mit Aufgaben zur Technischen Mathematik vertieft. Hier finden Sie Lösungsvorschläge. Themen: Kolbenkraft, Drehmoment, Öldruck, Wirkungsgrad, Flächenpressung, Abscherfestigkeit, Ölgeschwindigkeit.

Lernprojekt Spannvorrichtung:
Lösung Aufgaben Technische Mathematik

Aufgabe 1:  

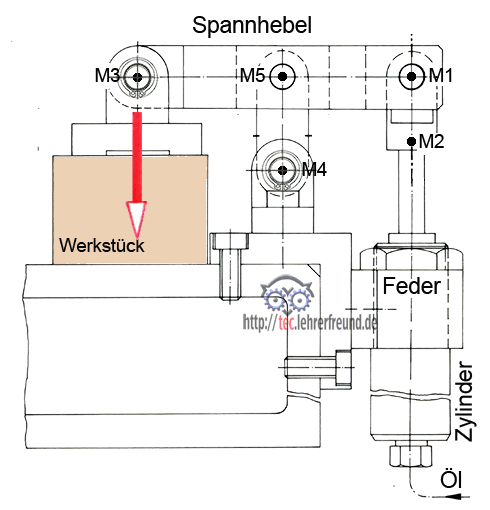
1a) Das Werkstück wird mit F_Sp = 1750 N auf den Maschinentisch gedrückt. 
Welche Kolbenkraft F_K ist dafür erforderlich, wenn die Feder im zusammengedrückten Zustand F_F = 45 daN erzeugt?
In der Skizze sind die auf den Spannhebel wirkenden Kräfte eingetragen.

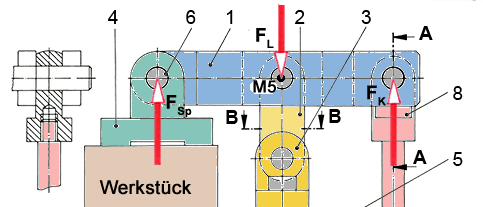
Lösungsvorschlag 

ΣM_M5 = 0 = F_Sp • 55 mm – (F_K – F_F) • 50 mm 

(F_K – F_F) • 50 mm =  F_Sp • 55 mm 

F_K – F_F = F_Sp • 55 mm : 50 mm = 

F_K = F_Sp • 55 mm : 50 mm + 450 N 

F_K = 2 375 N 

1b) Mit den Zahlen von 1a): Mit welcher Kraft F_L wird die Lasche nach oben gezogen, wenn das Werkstück gespannt ist? 

Lösungsvorschlag

ΣF_y = 0 = F_Sp – F_L + (F_K – F_F) 

F_L = F_Sp + (F_K – F_F) 

F_L = 1750 N + 2 375 N – 450 N 

F_L = 3 675 N

1c) Spannzylinder. Der Kolben hat einen Durchmesser 22 mm. Welcher Öldruck ist erforderlich, um den Widerstand F_K – F_F zu überwinden? 

Lösungsvorschlag 

Kolbenkraft F_K = A • p 

p = F_K : A  ––> A = d² • π / 4 = (2,2 cm)² • 3,14 / 4 = 3,8 cm² 

p = 237,5 daN : 3,8 cm² 

p = 62,5 bar

1d) In Aufgabe 1c) soll ein Wirkungsgrad µ = 85% berücksichtigt werden. Berechnen Sie den Öldruck für diesen Fall. 

Lösungsvorschlag

μ = F_ab : F_zu;   F_ab = 2375 N;  F_zu = am Kolben wirkende Kraft aus Öldruck.

F_zu = F_K = F_ab : μ

F_zu = 2 375 N : 0,85 = 2 794 N 

p = F_K : A = 279,4 daN : 3,8 cm²

p = 73,5 bar 

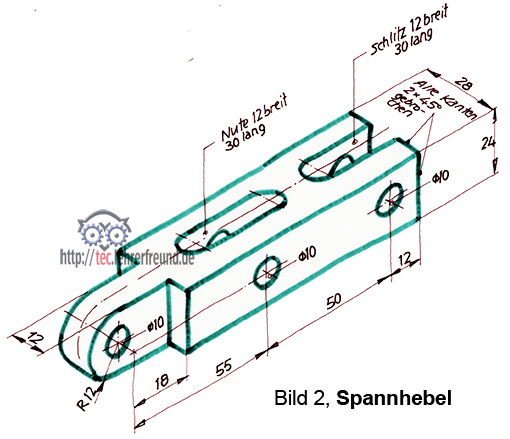
Aufgabe 2: Spannpratze 4 

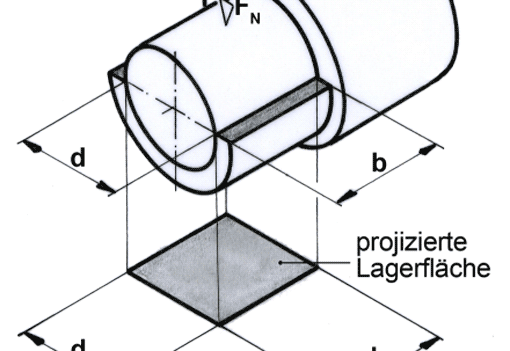
2a) An den vier Sohlen der Spannpratze soll die Flächenpressung den Wert p_F = 5 N/mm² nicht übersteigen. Wird der Wert erreicht? 

Lösungsvorschlag

F_Sp = 1750 N; A = 4 • (1,2 cm)² = 5,76 cm² 

p_Fl = F_Sp : A = 1750 N : 5,76cm² = 303,8 N/cm² 

p_Fl = 3,04 N/cm₂ 

Die Flächenpressung p_Fl bleibt unter dem max. zulässigen Wert p = 5 N/cm² .

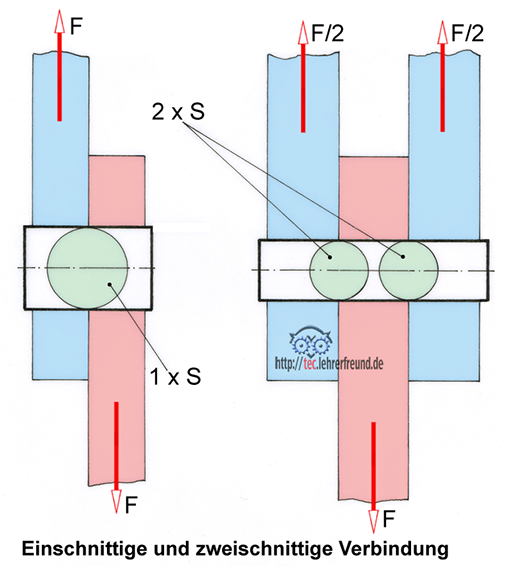
2b) Die Achsen der Spannvorrichtung werden auf Abscherung beansprucht. 
– Wie hoch ist die Scherspannung in der Laschenachse? 
– Welcher Wert ist nach Tabellenbuch für einen Stahl C 45 zulässig, wenn eine Sicherheitszahl ν = 2 gefordert wird? 

(Ist der Wert für die Scherfestigkeit (τaB) nicht bekannt, erhält man bei Stählen einen Ersatzwert, wenn man ihre Zugfestigkeit (R_m) kennt: τ_aB = (0,6 bis 0,9) • R_m.)

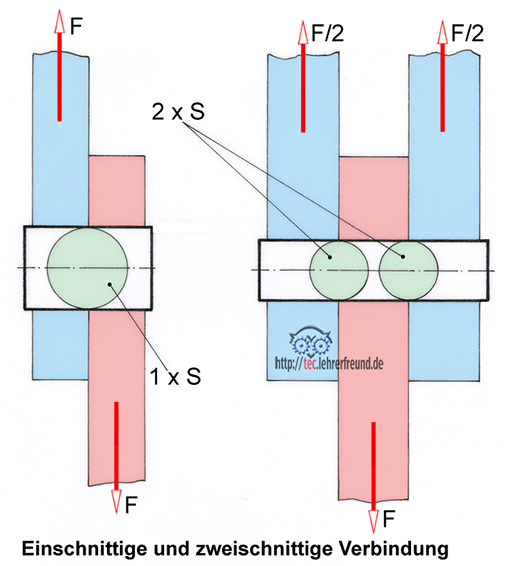
Lösungsvorschlag 

Scherspannung τ_a ( tau ) = F_L : A_a;  Achsenquerschnitt A_a = d² • π / 4 = (1 cm)² • 3,14 : 4 = 0,785 cm² 

τ_a = 3 675 N : 0,785 cm² = 4679 N/cm² 

τ_a = 46,79 N/mm² 

Für einen Stahl C 45 mit R_m = 420 N/mm² wäre ein τ_a = 420 N/mm² • 0,8 : 2 = 170 N/mm² zulässig. Mit τ_a = 47 liegt man also in der sicheren Zone.

Scherspannung: Lesen Sie im tec.LF hier nach

2c) Die Lasche schwingt im Lagerbock 7. Dieser ist mit 2 Schrauben M10, Festigkeitsklasse 8.8 auf dem Winkel 5 befestigt.  
Berechnen Sie
– welche zulässige Zugkraft eine Schraube M10 übertragen kann, wenn man mit einer Sicherheitszahl 2,5 rechnet, 
– welche Zugkraft auf eine Schraube wirkt, wenn F_L mit 4 000 N nach oben zieht. 

Lösungsvorschlag 

Was bedeutet 8.8? 

Die erste Zahl 8 bezieht sich auf die Mindestzugfestigkeit R_m. Die Zahl 8 wird mit 100 multipliziert: 8 • 100 = 800 N/mm²; dies ist R_m. 
Die zweite Zahl 8 bezieht sich auf die Mindeststreckgrenze R_e. Sie erhält man, wenn man die erste Zahl mit dem zehnfachen Wert mit der zweiten Zahl multipliziert: R_e = 8 • 80 = 640 N/mm². Weil R_e aus Sicherheitsgründen im Betrieb nicht erreicht werden darf, wird eine Sicherheitszahl ν (nü) eingeführt. 

(Schraubenfestigkeit: Lesen Sie im tec.LEHRERFREUND hier und hier nach.

σ_{z zul} = R_e : ν = 640 N/mm² : 2,5 = 256 N/mm² 

Der Spannungsquerschnitt A_s ist lt. Tabellenbuch 58 mm² 

Zulässige Schraubenkraft F_Szul = A_s • σzul = 58 mm² • 256 N/mm² 

F_Szul = 14 848 N 

Aufgabe 3:  
Das in den Zylinder fließende Öl soll im Zulaufrohr eine Geschwindigkeit von 4 m/s nicht überschreiten. 
Beim Spannen des Werkstücks fließt über das Zulaufrohr mit d_i = 5 mm Öl in den Kolbenraum. Welche Höchstgeschwindigkeit erreicht das Öl, wenn der Kolben (ø22 mm) mit v_K = 0,15 m/s ausfährt? 

Lösungsvorschlag 

V_K ist das Kolbenverdrängungs-Volumen pro Sekunde;
V_R ist das im Rohr zulaufende Volumen pro Sekunde 

V_K = V_R 

V_K = A_K • v_K =d² • π / 4 • v_K = (2,2 cm)² • 3,14 / 4 • 15 cm/s 

V_K = 57 cm³/s 

V_K = V_R = A_R • v_R ––> v_R = V_R : A_R = 57 cm³/s : (0,5 cm)² • π : 4 = 

v_R = 2,9 m/s