Werkstoffprüfung (2): Hookesches Gesetz, Elastizitätsmodul 05.05.2012, 07:01

Maschinen- und Bauteile verformen sich unter der Einwirkung von Kräften elastisch. Wirkt die Kraft nicht mehr, dann geht auch die Verformung vollständig zurück. Bei einer plastischen Dehnung dagegen verformt sich der Werkstoff bleibend; die Verformung geht nicht mehr vollständig zurück. Die Gesetzmäßigkeiten dazu beschreibt das Hookesche Gesetz.

Elastizitätsmodul, Hookesches Gesetz bei Zugbeanspruchung

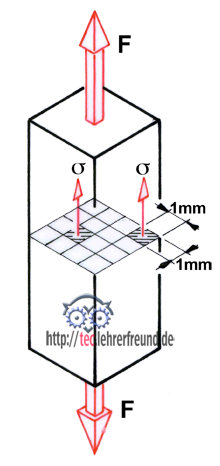
Für viele Festigkeitsrechnungen ist es wichtig, den Zusammenhang zwischen der Spannung σ (griech. sigma) und der zugehörigen Dehnung ε (griech. epsilon) zu kennen. Zieht man einen Gummifaden auseinander, dann erkennt man, dass mit zunehmender Spannung auch die Dehnung (Verlängerung ∆L) ansteigt. Versuche mit geeigneten Probestäben zeigen, dass bei vielen Werkstoffen die Dehnung ε mit der Spannung σ im gleichen Verhältnis (proportional) wächst. Bei doppelter Spannung σ zeigt sich dann auch die doppelte Dehnung ε. Man kann auch sagen: Das Verhältnis von Spannung σ und Dehnung ε ist für den Werkstoff ein bestimmter, in den für die Praxis wichtigen Spannungsgrenzen gleichbleibender Wert, der so genannte Elastizitätsmodul E. Er ist eine Stoffkonstante. Da die Dehnung ε eine unbenannte Zahl ist, hat E die Einheit der Spannung, also N/mm².   

Das beschriebene Verhalten beobachtet man sowohl bei Metallen als auch bei anderen harten und spröden Materialien wie Glas und Keramik.

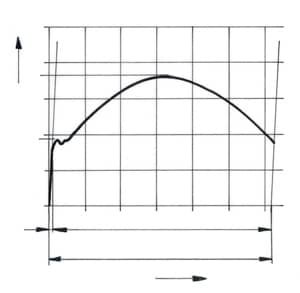
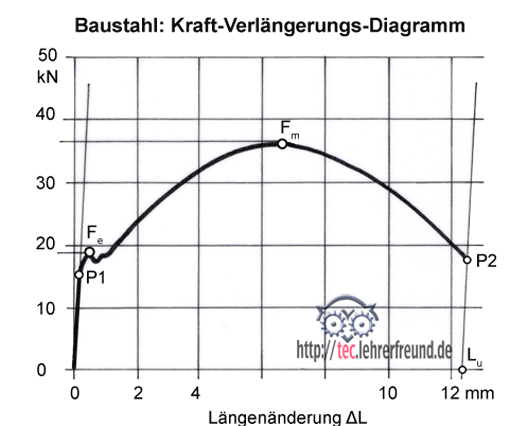
Das Spannungs-Dehnungs-Diagramm (siehe auch tec.LEHRERFREUND-Beitrag »Zugversuch«) gibt Auskunft über die Zugfestigkeit R_m, die Streckgrenze R_e und die Bruchdehnung A, aber auch über die elastische und die plastische Verformung der geprüften Werkstoffe.

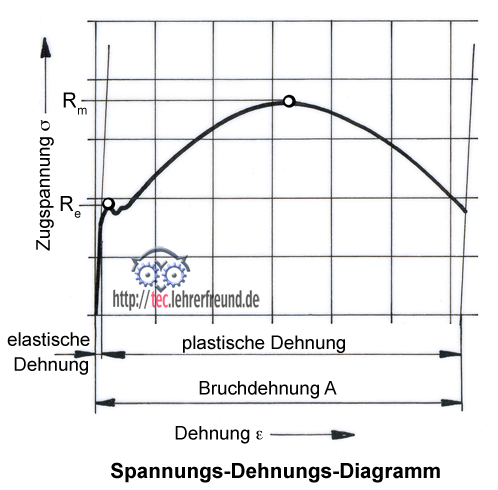
Bezeichnungen:

Kräfte und Spannungen

F Zugkraft 
σ₁, σ₂, σ₃ Zugspannungen
σ_E Elastizitätsgrenze
E Elastizitätsmodul
R_m Zugfestigkeit
R_e Streckgrenze

Flächen und Längen

S Anfangsquerschnitt
L₀ Anfangsmesslänge
∆L elastische Längenänderung
ε₁, ε₂, ε₃  elastische Dehnungen
A Bruchdehnung

Die Spannung steigt bis zur Elastizitätsgrenze σ_E geradlinig an, d. h. σ verändert sich im gleichen Verhältnis wie die Dehnung ε.
Die mathematischen Zusammenhänge kann man mit Hilfe des Strahlensatzes ermitteln.

Für das blaue Dreieck gilt: σ₁ : ε₁ = σ₂ : ε₂ = ∆σ : ∆ε = σ : ε = E = Elastizitätsmodul = konstant.

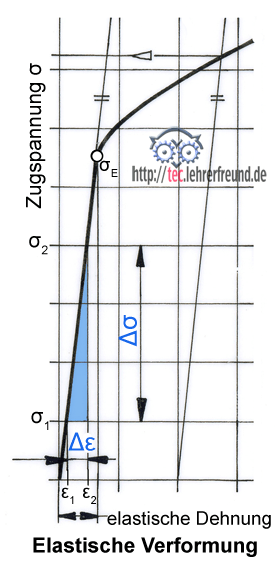
Aus diesen Beziehungen folgt das Hookesche Gesetz: σ = E · ε mit ε = ∆L/L₀. Darin ist der Elastizitätsmodul E ein Maß für die Steigung der gerade verlaufenden Spannungs-Dehnungslinie. Den Elastizitätsmodul kann man aus den Messwerten des Zugversuches berechnen. So ist der Elastizitätsmodul E bei Stahl 210 000 N/mm² und bei Cu-Legierungen 90 000 N/mm² (Mittelwerte).  

Um für die elastische Verlängerung ∆L eine Formel zu erhalten, in der nur Größen des Probestabs stehen, schreibt man im Hookeschen Gesetz
- für die Spannung σ = F/S und
- für die Dehnung ε = ∆L/L₀. Daraus ergibt sich ∆L = (F · L₀) : (S · E).  

Nachfolgend sind die wichtigsten Berechnungsformeln zusammengefasst:
Zugspannung   σ = F : S
Elastische Dehnung   ε = ∆L : L₀
Hookesches Gesetz   σ = E · ε
Elastische Verlängerung   ∆L = (F · L₀) : (S · E)


Rechenbeispiel:  
In einem Zugversuch soll der Elastizitätsmodul E ermittelt werden. Dafür werden Rundstäbe mit d = 8 mm und der Anfangsmesslänge L₀ = 40 mm verwendet. Auf dem geradlinig verlaufenden Kurvenast führt eine Belastung von 12 kN zu einer Stabverlängerung ∆L = 0,046 mm.

Zu berechnen sind:  
a) die Zugspannung σ
b) die elastische Dehnung ε
c) der Elastizitätsmodul E  

Lösungen:
a) Zugspannung σ = 238,73 N/mm²
b) elastische Dehnung ε = 0,00115
c) Elastizitätsmodul E = 207 591 N/mm² (dies entspricht Stahl mit einem Mittelwert von 210 000 N/mm²)

Übungsbeispiel: Ein 750 mm langer Zugstab aus S 235 JR (E = 210 000 N/mm²) mit dem Durchmesser d = 8 mm und wird mit F = 10 kN belastet.

Wie groß sind
a) der Querschnitt S des Zugstabs?
b) die elastische Verlängerung ∆L?

Lösungen:
a) Querschnitt S = 50,265 mm²
b) elastische Verlängerung ∆L = 0,71 mm 

__________________________________ 

Dazugehörige Themen: Zugfestigkeit, Biegefestigkeit, Flächenpressung 

Die Grafik unten ist für die Verwendung in Arbeitsblättern gedacht.