Kräfte am Vordach - Culmannsche Gerade üben 14.12.2011, 13:19

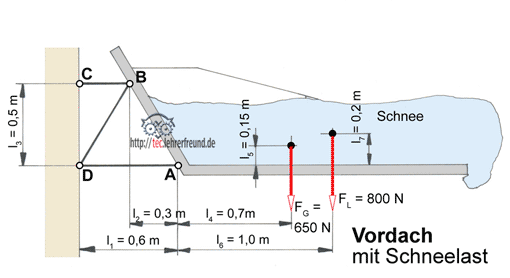
Ein Vordach muss außer seinem Eigengewicht eine Schneelast tragen. Wie stark werden dabei die Anlenkpunkte belastet? Auch hier hilft wieder die Culmannsche Gerade weiter.

Niveau: Technische Oberschule, Berufskolleg u. Ä.

Kräfte an einem Vordach

Aufgaben

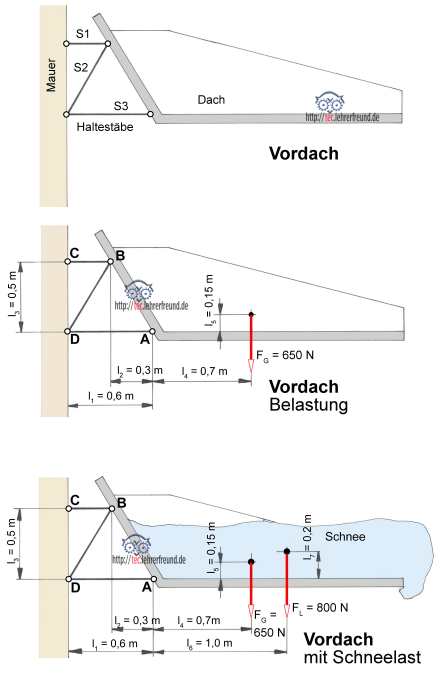
1. Das 650 N schwere Hausvordach ist mithilfe der Stäbe S1, S2 und S3 an der Hauswand befestigt. Wie groß sind die Stabkräfte?

2. Das Vordach muss eine Schneelast von 800 N tragen können (Abstände usw. siehe Skizze). Wie groß sind die Stabkräfte jetzt?

Die Aufgaben lösen wir wie folgt.

Aufgabe 1: Dach ohne Schneelast

a) Das Vordach freimachen.

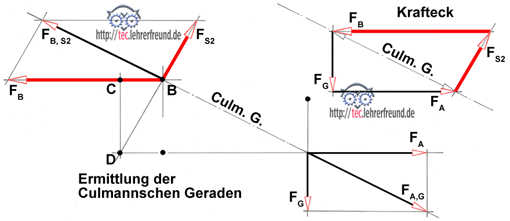
Dabei werden anstelle der Stäbe die auf das Vordach wirkenden Kräfte eingezeichnet. Man erkennt: Es sind die vier Kräfte F_G, F_A, F_B und F_S2. Um das Gleichgewicht von vier Kräften zu finden, benötigen wir die Culmannsche Gerade.

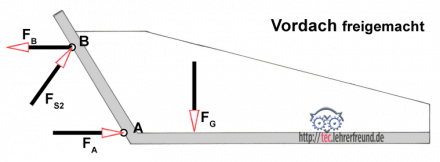
b) Die Stabkräfte F_B und F_S2 zeichnerisch ermitteln.

Wir konstruieren die Culmannsche Gerade C.G. Sie geht davon aus, dass wir zwei Kräfte mit möglichst hohem Informationsgehalt zum Schnitt bringen. Das sind die Kräfte F_G und F_A. Von F_G kennen wir Richtung und Größe, von F_A nur die Richtung. Das Kräfteparallelogramm ergibt sich aus der Richtung der C.G.
Am Punkt B greifen zwei weitere Kräfte an: F_B und F_S2. Die Resultierende von F_A und F_G muss auch die Resultierende von F_B und F_S2 sein, allerdings mit entgegengesetzter Richtung. Beide Resultierende liegen auf derselben Wirkungslinie, die nichts anderes ist als die Culmannsche Gerade.

c) Das Krafteck mit den Kräften F_G, F_A, F_B und F_S2 zeichnen. Die vier Kräfte bilden eine geschlossenes Krafteck. Die Diagonale entspricht den Resultierenden F_A,G und F_B,S2.

Für die Pläne wurden folgende Maßstäbe gewählt (die auf der Webseite leider verzerrt erscheinen):

Lageplan: M_L =  0,2 m / 1 cm;   Kräfteparallelogramme: M_K = 300 N/ 1 cm

Ergebnisse (herausgemessen):

F_B = 1680 N   / F_S2 = 750 N   / F_A = 1245 N

2. Dach mit Schneelast 

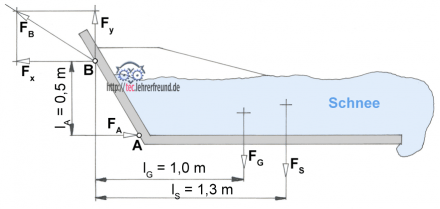
 I. Waagrechte Kräfte Σ F_x = 0 = F_A -  F_x

II. Senkrechte Kräfte Σ F_y = 0 = F_y  – F_G - F_S

III. Momentengleichung um den Punkt B: Σ M_(B) = 0 = F_A · l_A –  F_G · l_G – F_S · l_S 

Aus III.: F_A · l_A =  F_G · l_G + F_S · l_S

F_A =  (F_G · l_G + F_S · l_S) :  l_A  = (650 N · 1,0 m + 800 N · 1,3 m) : 0,5 m

F_A = 3380 N

Aus I.: F_x = F_A = 3380 N 

Aus II.: F_y = F_G + F_S = 1450 N 

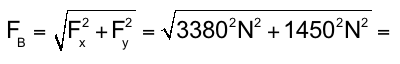
F_B = 3678 N 

_________________

Die Skizze unten könnte für ein Arbeitsblatt verwendet werden.