Zahnräder, Getriebe (Teil 1) 31.05.2008, 00:08
Hier finden Sie eine Kurzbeschreibung von Einzelzahnrädern und Getriebearten (Stirnrad, Kegelrad, Schneckenrad, Planetengetriebe) .
3. und 4. Ausbildungsjahr
Hier finden Sie Informationen zum Einzelzahnrad (Stirnrad). Danach beschreibt eine Übersicht den Aufbau und die Eigenschaften von Stirnrad- und Kegelradgetrieben.
In »So rechnet man‘s« berechnen wir Einzelzahnräder und Stirnradgetriebe. Mit Zeichenaufgaben in »So zeichnet man‘s« gehen wir auf die Darstellung von Zahnrädern ein. Alle Aufgaben setzen Grundlagen im Zeichnen und Rechnen voraus. Eine wichtige Hilfe beim Lösen der Aufgaben ist das Tabellenbuch.
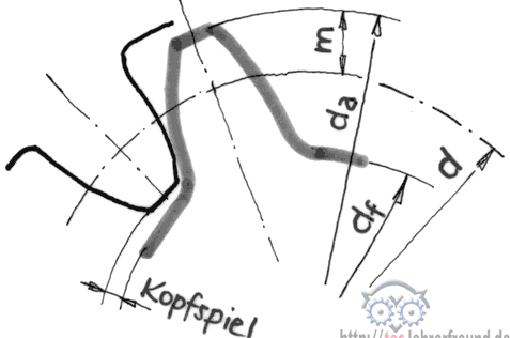
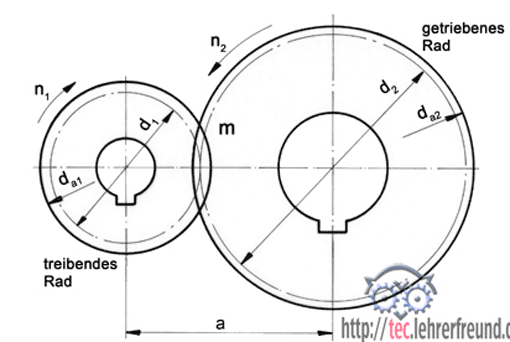
1. Aufbau des Einzelzahnrads (Stirnrad)
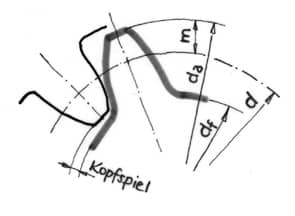
Der Zahn besteht aus dem Kopf und dem Fuß. Dazu gehören Durchmesser und Höhen: Kopfkreisdurchmesser, Fußkreisdurchmesser, Zahnkopfhöhe und Zahnfußhöhe. In der Mitte, aber leicht zum Kopfkreisdurchmesser hin verschoben, liegt der Teilkreisdurchmesser. Alle Zahngrößen bauen auf dem Modul m auf (siehe Technische Mathematik).
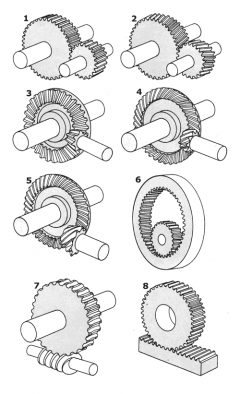
2. Zahnradformen
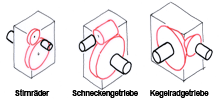
In den gängigen Getrieben aller Technikbereiche findet man vorwiegend drei Zahnradformen.
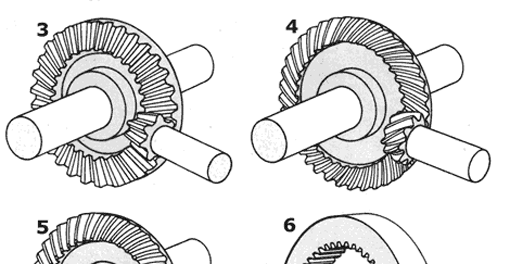
Stirnräder (Zeichnungen 1 und 2), Kegelräder (Zeichnungen 3 bis 5) und die Schnecke mit Schneckenrad (Zeichnung 7). Planetengetriebe 6 und Zahnstangengetriebe 8 zählen zu den Stirnradgetrieben.
Die unterschiedlichen Radformen ergeben sich zwingend aus der Lage von An- und Abtriebsachse zueinander. Beim Differential etwa muss die Getriebedrehrichtung aus der Maschinen-Längsachse um 90° zu den Hinterrädern umgelenkt werden: Dies ist ein Fall für Kegelräder. Man kann Folgendes festhalten: Stirnräder setzt man ein, wenn die Antriebs- und Abtriebsachse parallel zueinander liegen; bilden sie einen Winkel zueinander und liegen sie dabei auf derselben Ebene (man sagt dann, die Achsen »schneiden« sich), dann muss mit Kegelrädern gearbeitet werden. »Überkreuzen« sich die Achsen in der Art einer Straßenunter- und -überführung, dann wird man sich eines Schneckengetriebes bedienen. Neben der Lage der Achsen spielen beim Einsatz eines Zahnradgetriebes weitere Überlegungen eine Rolle: das zu übertragende Drehmoment, das Übersetzungsverhältnis, die Eigenhemmung, der Platzbedarf usw..
Exkurs: Evolvente
Die Grundform der Zahnflanken ist die Evolvente, zu deutsch Fadenlinie.
Die Evolvente verleiht Zahntrieben folgende Eigenschaften:
- Beim Abrollen der Zähne aufeinander bleibt des Übersetzungsverhältnis in jeder Lage konstant,
- Zwischen den Flanken gibt es eine nur geringfügige gleitende Reibung,
- Die Druckverteilung zwischen den Flanken ist optimal,
- Die Zähne zwischen Antriebs- und Abtriebsrad klemmen nicht.
Stirnräder
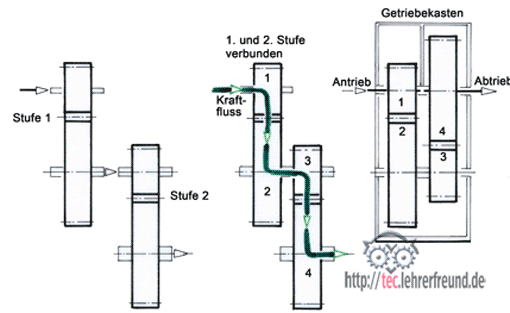
Bei Getrieben, die hohe Leistungen zu übertragen haben, überschreitet das Übersetzungsverhältnis i zwischen zwei Rädern selten den Wert 3 : 1 = 3,0. Muss es höher sein, ordnet man zwei oder mehr Stufen hintereinander an. Eine Stufe besteht aus einem Zahnradpaar. Wird ein so genanntes Zwischenrad verwendet, hat dieses keinen Einfluss auf das Übersetzungsverhältnis: Es ändert lediglich die Abtriebsrichtung. Dies ist ein Grund, warum man es in allen Rückwärtsgängen findet.
Schräg verzahnte Stirnräder
Verlaufen die Zähne in der gleichen Richtung wie die Achse, dann ist das Rad gerade verzahnt (Bild 1). Solche Verzahnungen laufen relativ laut und neigen bei höheren Drehzahlen zum Vibrieren. Die in dieser Hinsicht günstigere Schrägverzahnung (Bild 2) liegt vor, wenn die Zähne einen Winkel zur Achse bilden.
Die Schrägverzahnung unterscheidet sich von der Geradverzahnung in drei wichtigen Eigenschaften:
- Wegen dem allmählichen Zahneingriff läuft die Schrägverzahnung sehr geräuscharm,
- die größere Auflagefläche an den Zahnflanken kann mehr Kraft übertragen als gleich große, gerade verzahnte Zähne,
- bei der Schrägverzahnung - und dies ist meist ein Nachteil - tritt eine Kraftkomponente in axialer Richtung auf, die eine entsprechende Lagerung erfordert (axial = in Richtung der Achse liegend; radial = in Richtung des Radius liegend). Wo solche Axialkräfte zu groß werden, kann man sie mit Hilfe einer doppelten Schrägverzahnung oder einer »Pfeilverzahnung« aufheben.
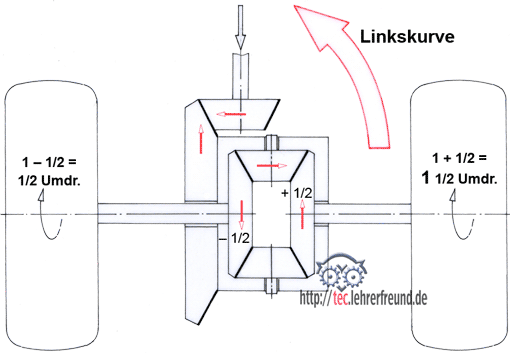
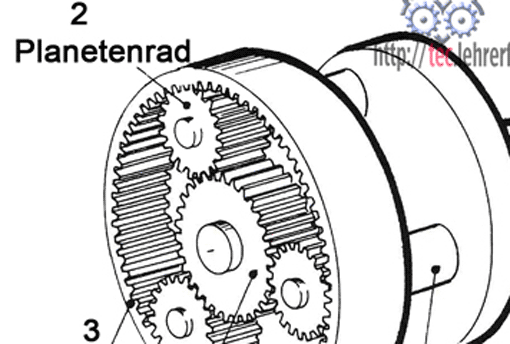
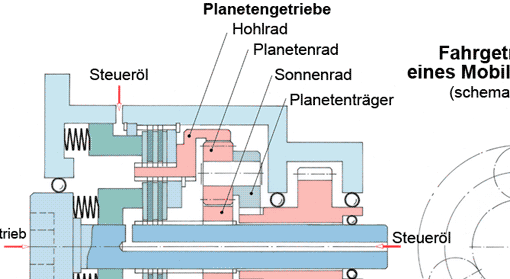
Räder in Planetengetrieben
Planetengetriebe mit Sonnenrad 1, Hohlrad 3, Planetenträger 4 und Planetenrad 2 sind ebenfalls Stirnradgetriebe. Die Übersetzungen solcher Getriebe werden dadurch erreicht, dass jeweils ein Bauteil angetrieben und ein anderes festgehalten wird.
Beispiel (Bild): Das Hohlrad 3 wird festgehalten, das Sonnenrad 1 treibt an. Der Abtrieb läuft über den Planetenträger.
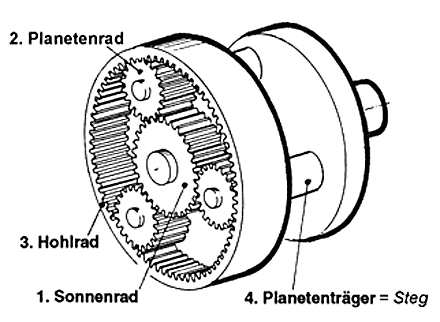
Planetengetriebe besprechen wie ausführlicher in einem gesonderten Kapitel.
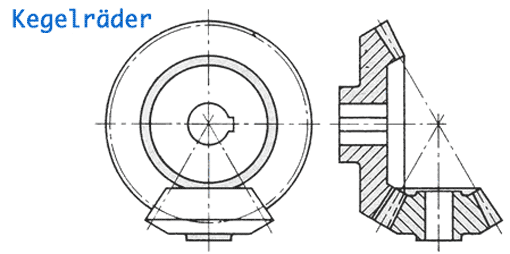
Kegelräder
Es gibt geradverzahnte und bogenverzahnte Kegelräder. Die letzteren - im Falle einer Achsversetzung auch als Hypoidräder bezeichnet - besitzen ähnliche Eigenschaften wie schräg verzahnte Stirnräder. Bogenverzahnungen findet man häufig in Differentialgetrieben. Das Kennzeichen der Hypoidverzahnung ist das nach unten versetzte Antriebskegelrad.
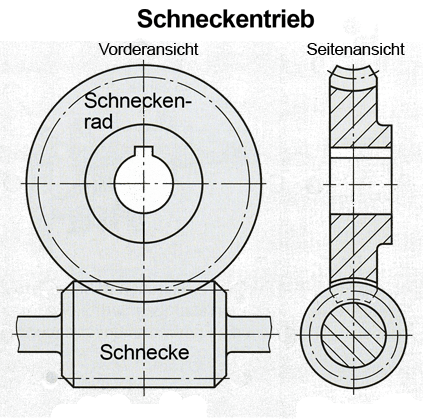
Schnecke und Schneckenrad
Bei Schneckengetrieben nutzt man den großen Vorteil, dass sie mit einer einzigen Stufe Übersetzungsverhältnisse bis i = 40 : 1 zulassen. Diesen Vorteil muss man allerdings mit hoher Gleitreibung erkaufen. Um die daraus resultierende Verschleißgefahr in Grenzen zu halten, ist auf aufeinander abgestimmte Zahnradwerkstoffe zu achten. Hoch belastete Schneckentriebe laufen außerdem im Ölbad.
Die Schnecke wird meist aus gehärtetem Stahl, das Schneckenrad aus Grauguss oder Bronze hergestellt. Schneckengetriebe eignen sich auch dort, wo Selbsthemmung wichtig ist, d.h. wo das Getriebe nicht rückwärts läuft, wenn es belastet wird. Dies spielt beispielsweise bei Hebezeugen eine Rolle.