Papierlocher, Übung zur Culmann-Geraden (2) 03.01.2012, 11:56
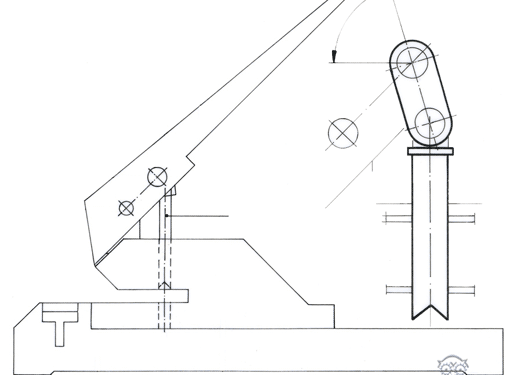
Zeichnerischer Lösungsvorschlag zum Beitrag »Papierlocher, Übung zur Culmann-Geraden (1)«. Mit unvollständigen Skizzen für ein Arbeitsblatt.
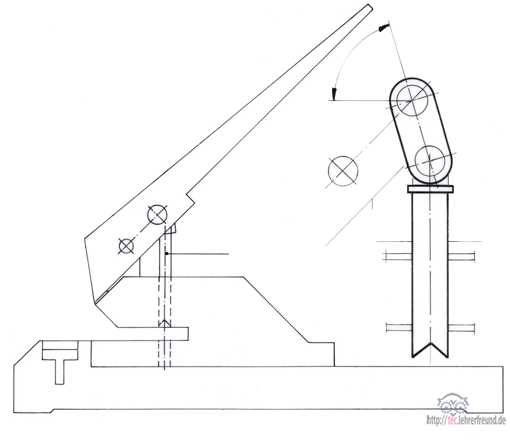
Papierlocher
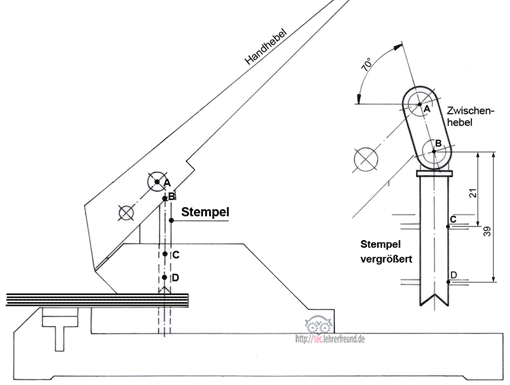
Der Handhebel des Lochers übt auf den schrägen Zwischenhebel eine Druckkraft aus. Diese drückt über FB den Lochstempel nach unten gegen den zu lochenden Papierstapel.
Aufgabe:
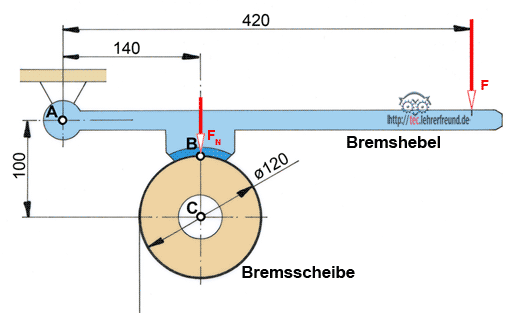
Ermitteln Sie zeichnerisch alle auf den Stempel wirkenden Kräfte, wenn FB = 500 N ist.
a) Machen Sie dazu den Stempel frei. Gehen Sie davon aus, dass die bei C und D wirkenden Kräfte waagrecht angreifen. Nähere Informationen dazu gibt der tec.LEHRERFREUND-Beitrag »Kräfte freimachen«.
b) Ermitteln Sie zeichnerisch die Größen und Richtungen der auf den Stempel wirkenden Kräfte.
Lösungsvorschlag
a) Stempel freimachen: FB wirkt unter 70° von oben auf den Stempel. Die sich daraus ergebenden seitlichen Kräfte werden von der Stempelführung in C und D aufgefangen (Kräfte FC und FD). Vom zu lochenden Papierstapel her wirkt die senkrechte Stempelkraft FS.
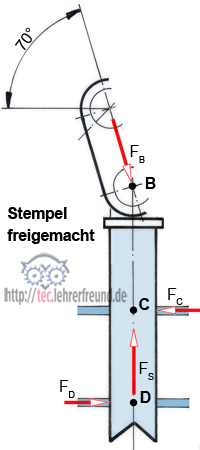
b) Wir ermitteln zeichnerisch die Größen und Richtungen der auf den Stempel wirkenden Kräfte.
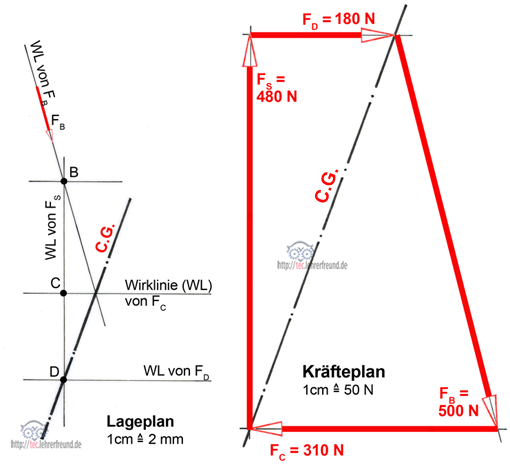
Dazu konstruieren wir zuerst den maßstäblichen Lageplan. Die Culmannsche Gerade geht durch die Schnittpunkte je zweier Kräfte-Wirklinien. Hier ist es der Schnittpunkt der Wirklinie von FB und FC (oben) und der Schnittpunkt der Wirklinien von FD und FS (unten).
Der Kräfteplan besteht aus einem sich schließenden, aus FB, FC, FD und FS bestehenden Krafteck:
- Schritt 1: Culmannsche Gerade aus dem Lageplan durch Parallelverschiebung übertragen.
- Schritt 2: Kraft FB an die Culmannsche Gerade ansetzen. Diese Kraft ist - im Gegensatz zu den anderen 3 Kräften - vollständig bekannt.
- Schritt 3: Am Ende von FB die Wirklinie von FC anfügen. Diese Kraft endet an der Culmannschen Geraden.
- Schritt 4: Mit den Wirklinien von FS und FD fortfahren und so das Krafteck schließen.
- Schritt 5: Die Längen der Kraftpfeile messen und mit dem Kräftemaßstab umrechnen.
Wiederholung zum Thema Culmannsche Gerade:
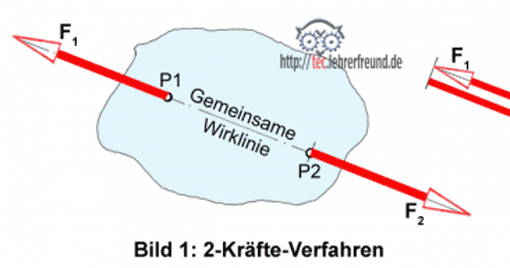
Vier nicht parallele Kräfte sind im Gleichgewicht, wenn die Resultierenden je zweier Kräfte ein geschlossenes Krafteck bilden und eine gemeinsame Wirklinie — die Culmannsche Gerade — haben (4-Kräfte-Verfahren).
Man löst die Aufgabe, indem man den Lageplan zeichnet und dort die Wirklinien je zweier Kräfte zum Schnitt bringt. Hier sind es die Wirklinien der Kräfte FS und FD, und von FB und FC. Damit ist die Culmannsche Gerade gefunden und der Kräfteplan kann gezeichnet werden.
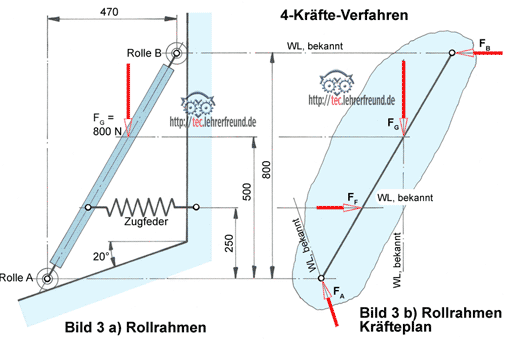
Nun zeichnet man die gegebene Kraft FB maßstäblich, überträgt die Culmannsche Gerade vom Lage- in den Kräfteplan, indem man sie durch Anfangspunkt von FB laufen lässt. Man schließt dieses Krafteck durch die zugehörige Kraft FC. Das erste Krafteck besteht also aus den Kräften FB, FC und der Resultierenden FB,C. In gleicher Weise lässt sich nun das zweite Krafteck mit den Kräften FS, FD und FS,D zeichnen.
Der Richtungssinn der Kräfte ergibt sich aus der Bedingung des »geschlossenen Kräftezugs«, d. h. der Umfahrungssinn des Kraftecks muss, von FB ausgehend, beibehalten werden.
___________________
Die Skizze unten könnte für ein Arbeitsblatt verwendet werden.