- Technik des Alltags
- Maschinenelemente, Funktionsgruppen
- Verbrennungsmotoren
- Werkzeugmaschinen
- Versuche im Unterricht
- Technische Kurven zeichnen
- Schnittdarstellungen im Technischen Zeichnen
- Zeichnungen bemaßen
- Zeichnungs-Normung
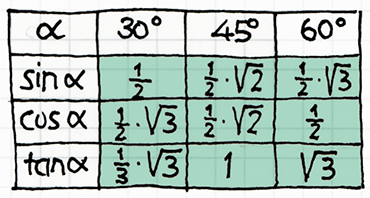
- Grundlagen der Technischen Mathematik
- Druck
- Elektrotechnik
- Festigkeitslehre
- Geschwindigkeit
- Kräfte
- Reibung
- Statik
- Frühe Technik
- Baumaschinen
- Elektrik
- Hydraulik
- Hydraulische Antriebe
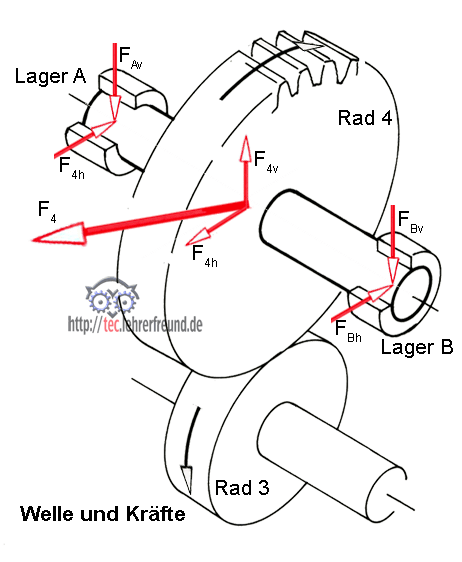
- Kräfte und Drehmomente
- Kupplungen
- Werkstoffe
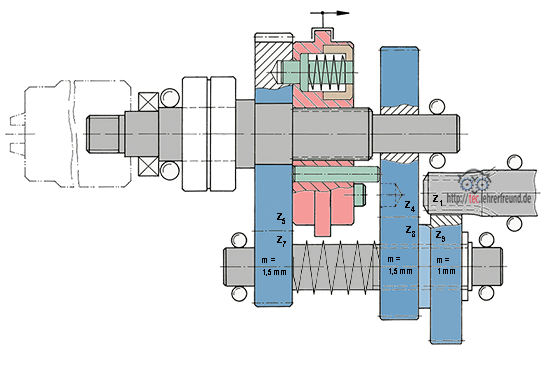
- Zahnräder
- prima.tec - Technik für Kinder
- Alles …
Technische Mathematik
Mit Hilfe der Technische Mathematik vergewissert sich der Techniker, ob das, was er tut, technisch möglich ist. Das gilt für den Mechaniker auf einer unteren Stufe ebenso wie für den Meister, den Konstrukteur oder den Ingenieur.
<Anzeige
Anzeige
Anzeige
Anzeige
> 646 Einträge, 952 Kommentare. Seite generiert in 0.2803 Sekunden bei 98 MySQL-Queries. 193 Lehrer/innen online (3 min Timeout / 1674 ) |